Last updated on 2018-8-1…
本文是对THU的Peng Cui所撰《A Survey on Network Embedding》一文的笔记,作梳理用。 (在此特别感谢舍友@YU对原文的翻译工作!)
(传统)基于图结构G=(V,E)的网络表示方法
- 高昂的计算复杂度:
- 上亿节点之间的边连接关系全部保存在边集 E 中, 许多算法都会对边集 E 进行迭代或者进行某些排列组合操作, 这无疑具有高昂的计算代价.
- 并行性较低:
- 节点之间因为边集 E 的存在而高度耦合, 因此将节点进行分布式计算处理较为困难.
- 无法适用机器学习方法:
- 大部分机器学习或深度学习算法都假设样本都可以在同一向量空间内独立表达.
- 然而由于边集 E 的存在, 图结构中的节点相互关联无法使用向量表示.
- 也许我们可以直接根据邻接矩阵给出节点的向量表示, 但是在具有上亿节点的网络中, 这样的稀疏向量表示是毫无意义的.
网络嵌入方法(network embedding)
为了解决传统网络表示方法带来的问题, 学习网络中节点的低维表示是一种新的解决方案.
在网络嵌入空间(network embedding space)内, 节点之间最初的关系, 如边或是其他高阶拓扑度量, 转变为向量空间内的距离,
而节点的拓扑或是结构属性则被编码为嵌入向量. 如下图所示是将 Karate 数据嵌入到二维空间内的表示.
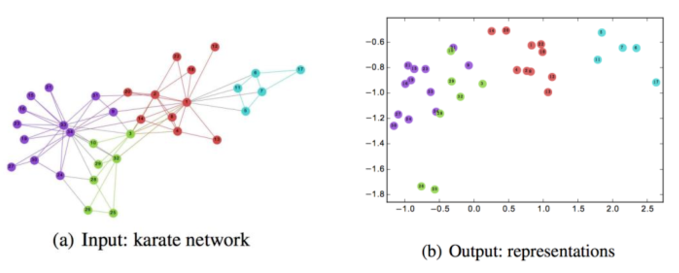
网络嵌入后的网络表示, 可以被用于分类、聚类、可视化和链路预测等. 网络嵌入与传统网络表示的比较如下图所示.
传统的网络表示直接利用观察到的邻接矩阵, 往往包含噪声和冗余信息.
而网络嵌入则首先学习低维空间中网络的稠密又连续的表示, 在这一过程可以降低噪声和冗余信息的影响.
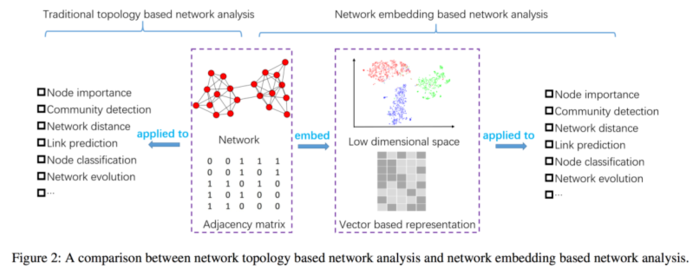
网络嵌入有两个目标:
- 网络重构, 该目标要求如果两个节点存在边, 那么在嵌入空间内它们也应当有着相对较小的距离.
- 学习出的嵌入空间应当有效支持网络推断, 如预测边、识别重要节点以及推断节点标签等.
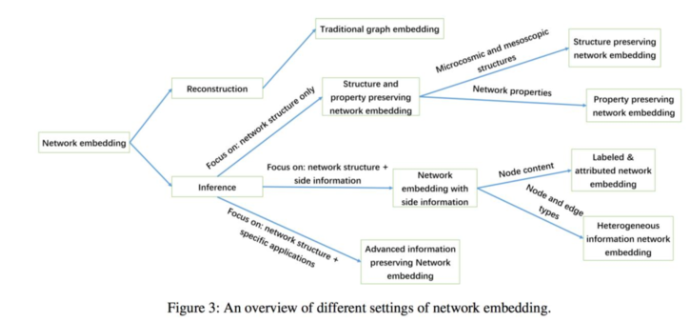
一、网络结构和属性保留的网络嵌入方法(network structure and properties preserving network embedding)
结构保留的网络嵌入方法(Structure Preserving Network Embedding)
网络结构通常可以划分为邻居结构、高阶节点近似性以及网络社区结构. 针对不同结构有不同的网络嵌入方法.
1.邻居结构和高阶节点近似性(Neighborhood Structures and High-order Node Proximity)
DeepWalk(Perozzi, Al-Rfou, and Skiena 2014)在保留节点的邻居结构的同时学习网络中的节点表示. 该算法发现在短随机游走中的节点分布与 NLP 中的词分布相似, 采用词表示学习中的 Skip-Gram 模型来学习网络的节点表示.Node2Vec(Grover and Leskovec 2016)指出 DeepWalk 不能不很好的捕捉网络中多样化的连接模式, Node2Vec定义一个灵活的节点邻居概念, 并结合深度优先采样和广 度优先采样, 使用二阶随机游走采样邻居节点. Node2Vec 对于同一社区内以及在网络中扮演相似角色的节点会学习出相似的嵌入表示.LINE(Tang et al. 2015)适用于大规模网络嵌入问题, 并且 LINE 可以同时保留节点的一阶和二阶近似性. 一阶近似性就是边信息等可以直接观察到的节点对关系, 二阶近似性则由两个节点的上下文(邻居)相似性来决定, 如下图所示, 节点 5、6 具有二阶近似性.GraRep(Cao, Lu, and Xu 2015)则指出只保留一、二阶近似性也不够, 提出了 k-step 近似性, 通过邻接矩阵A的k次相乘得到k-step后的转移概率矩阵, 随后修改Skip-Gram模型的损失函数利用 k-step 转移概率矩阵学习出节点的表示.
2.网络社区结构(Network Communities)
- Wang et al. (Wang et al. 2017) 提出了适用于网络嵌入的模块化非负矩阵分解模型(
MNMF), 该模型旨在同时保留网络微观结构 (一、二阶节点近似性) 和介观结构 (社区结构). 通过使用 NMF 模型对节点对相似性矩阵进行分解学习出低阶节点表示, 与此同时基于相似节点倾向于在同一社区内这一假设, Wang 等构建了一个社区表示的辅助矩阵将节点表示和社区结构联系到一起. - 上述所有模型皆为浅层模型, SDNE(Wang, Cui, and Zhu 2016)提出了深层网络嵌入模型, 其框架如上图所示,
SDNE使用深度自动编码器和多重非线性层来保留节点的邻居结构. 在编码器中间层使用 Laplacian eigenmaps 来保留节点一阶近似性, 而二阶近似性则依靠修正的自动编码器重构误差来保留. - 为了避免传统采样策略如随机游走的超参数对结果影响的问题, Cao 等使用
PageRank模型来初始化节点表示的有权转移概率矩阵 PCO, 随后计算出 PPMI 矩阵(Levy and Goldberg 2014), 最后使用集成去噪自动编码器(SDAE)来学习节点潜在表示.
属性保留的网络嵌入方法(Property Preserving Network Embedding)
大多数属性保留的网络嵌入方法都关注各类网络中的传递性和以及符号网络中的结构平衡属性.
- Ou et al. (Ou et al. 2015) 提出保留
非传递性属性, 所谓非传递性属性, 有节点 A, B, C 如果(A, B), (B, C)是相似节点对, 那么(A, C)就属于不相似节点对. 在现实中的例子为 学生的同学和亲友很可能没有联系. Ou 等通过线性映射构建了 M 个哈希表, 存放节点对之间的 M 种相似性, 最后对 M 中相似性做聚合处理获得语义相似性(semanticsimilarity), 聚合的标准是如果两个节点语义相似, 那么 M 个表中至少有一个相似性值很大, 否则它们不具有语义相似性. HOPE(Ou et al. 2016) 算法则保留了有向网络中非对称传递属性, 非对称传递性指, 如果节点 i有指向 j的一条边, 节点 j有指向 v的一条边, 那么很可能存在 i指向 v的 边但不一定有 v 指向 i 的边. 为了捕捉这种高阶近似性, HOPE 结合了四种度量 Katz Index、Rooted PageRank、Common Neighbors 和 Adamic-Adar, 这样获取的节点高阶近似性可以直接被 SVD 应用以获取低维嵌入表示.SiNE(Wang et al. 2017) 针对符号网络, 同时考虑网络中的正负边. 在符号网络中的结构平衡性定义如下, 一个节点三元组(𝑣 𝑗 , 𝑣 𝑘 ,𝑣 𝑙 ), 如果𝑒 𝑗𝑘 = 1, 𝑒 𝑗𝑙 = -1, 那么节点 i 和 j之间的相似性应当大于 i 和 k 的相似性. SiNE 使用了两个非线性激活函数的深度网络来学习网络嵌入表示.
二、带有辅助信息的网络嵌入方法(network embedding with side information)
除了结构信息, 辅助信息是网络嵌入的另一个重要信息源, 辅助信息通常可以分为两类:节点内容, 节点和边的类型.
带有节点内容的网络嵌入(Network Embedding with Node Content)
在某些类型的网络中如何信息网络, 节点信息往往和丰富, 包括节点标签, 属性甚至是其语义描述. 如何在网络嵌入的过程结合这些信息具有有趣性.
- Tu et al. (Tu et al. 2016) 利用节点标签信息提出了一个半监督网络嵌入算法
MMDW.MMDW 使用基于 DeepWalk 的矩阵分解, 并结合节点标签信息使用 SVM 寻找一个分类边界. 通过同时使 SVM 的 margin 和基于 DeepWalk 的矩阵分解达到最优结果,MMDW 学习出更有效的节点表示. - Le et al. (Le and Lauw 2014) 提出一个
文档网络(document network) 的生成式嵌入模型, 该模型同时考虑单词与文档, 文档和文档之间的关系. 除了学习可以重构网络的低维嵌入节点表示, 该模型还基于关系主题模型 (RTM) 在主题空间 (topic space) 内学习节点表示, 将两者结合得出最终的生成式模型. - Yang et al. (Yang et al. 2015) 提出
TADW算法, Yang 等首先证明 DeepWalk实际上是一种矩阵分解模型, 随后基于这个矩阵分解模型, 采用矩阵补全的思想把辅助信息融入矩阵分解过程. - Pan et al. (Pan et al. 2016) 提出一个结合网络结构、节点属性和节点标签信息的耦合深度模型
TriDNR. 其框架如下图所示, 考虑输入的网络包含节点集 V, 每个节点关联一个单词集 W, 同时一些节点存在不同的标签属性集 C, 模型同时学习节点之间的关系, 节点与单词的关系以及标签与单词的关系. LANE(Huang, Li, and Hu 2017) 也是一种考虑标签信息的网络嵌入算法, 与前面的算法不同, LANE 主要基于谱技术(spectral techniques), LANE 使用余弦相似度来构建节点属性、网络结构和标签的相似性矩阵. 根据三种相似性矩阵可以学习出三种不同的潜在表示, 为了将这三种潜在表示结合起来, LANE 将这三种表示投影到一个共同的空间内.
异质信息网络嵌入(Heterogeneous Information Network Embedding)
异质网络包含不同类型的节点和边. 如何结合这些不同类型的节点和边信息成为一个具有挑战性的问题.
- Yann et al. (Jacob, Denoyer, and Gallinari 2014) 提出了一个用于节点分类的异质社会网络嵌入算法, 在同一向量空间内学习所有类型的节点的表示, 并在这一空间内进行推断.
- Chang et al. (Chang et al. 2015) 提出了一个异质网络嵌入的深度模型. 即给定一个异质网络, 例如包含 image 和 text 两类的异质网络, 存在三种边, image-image,image-text, text-text, 三种边使用三种深度网络结构来学习潜在表示, 最后通过一个线性嵌入映射到统一向量空间内.
- Huang and Mamoulis (Huang and Mamoulis 2017) 提出了一个
元路径(meta path)相似性保留的异质网络嵌入算法. 基于截断元路径, 使用类似 LINE 的处理方法(分为一、二阶近似性)得到异质网络的嵌入表示. - Xu et al. (Xu et al. 2017) 提出了一个耦合异质网络的嵌入算法. 耦合异质网络包含两个相关但不同的异质网络, 对于每个异质网络使用 LINE 的处理方法获取节点表示,随后利用两个异质网络之间的 inter-network 边作为补充信息, 引入一个 harmonious嵌入矩阵来度量两个异质网络中的节点相似性学习出最终的嵌入表示.
三、高级信息保留的网络嵌入方法(advanced information preserving network embedding)
与辅助信息不同, 高级信息涉及到特定分析任务中的监督或伪监督信息(supervised or pseudo supervised information). 高级信息保留的网络嵌入方法主要分为两步: 首先是保留网络结构学习出嵌入表示, 其次是建立学习出的表示和特定任务的联系. 前者和网络结构和属性保留的网络嵌入方法没有太大不同, 后者则需要考虑相应的领域知识.
信息扩散(Information Diffusion)
信息扩散现象广泛存在于社交网络中, 以往的相关研究大多在原始网络空间中进行.
- Simon et al. (Bourigault et al. 2014) 提出了一个用于信息扩散预测的社交网络嵌入算法. 其基本思想是把观察到的信息扩散过程映射到一个连续空间内使用扩散核建模的热扩散过程(a heat diffusion process modeled by a diffusion kernel in the continuousspace). 算法的目标是学习出的节点潜在表示能够很好地解释节点之间的级联现象(cascade, 即哪些节点之间关系密切容易迅速在其间进行信息扩散), 并且可以预测在指定时间间隔内级联大小的增长(predicting the increment of cascade size after a giventime interval).
- Li et al. (Li et al. 2017) 指出以往的级联预测问题都是基于特征工程, Li等提出了一个端到端的深度模型. 类似于 DeepWalk, Li 等使用随机游走在级联图上采样一系列路径, 随后使用 GRU 循环神经网络来学习这些路径的嵌入表示, 在此之后使用注意力机制对学习出的路径表示进行集成以获取级联图的表示, 一旦级联图的表示被学习到就可以使用多层感知机来输出预测的级联大小.
异常检测(Anomaly Detection)
网络中的异常检测问题目的在于推断结构不一致(structural inconsistencies), 也就是说寻找连接到具有不同影响社区的异常节点, 如下图的红色节点.
- Hu et al. (Hu et al. 2016) 提出了一个基于网络嵌入的异常检测算法, 其定义的节点向量中不同的元素对应于节点与不同社区的联系, 节点的向量表示由其所有的邻居节点的向量表示加权和得到. Hu 等假设存在边连接的节点之间社区关系应当相似, 并提出一个异常度量, 该值越大代表节点越可能是异常节点.
网络对齐(Network Alignment)
网络对齐的目的是建立来自不同网络的节点之间的对应一致性(correspondence)
- Man et al. (Man et al. 2016) 提出了一个预测跨越不同社交网络的
锚链接(anchor links)的网络嵌入算法. 所谓锚链接是指在不同社交网络中都出现的用户节点在网络之间自然产生的链接. 该问题描述为: 给定源网络、目标网络和观测到的一些锚链接, 判别存在两个网络之间的隐藏锚链接. Man等先学习出各自网络中的节点表示, 然后再学习线性或非线性映射函数如多层感知机来建立网络间节点的联系, 之后在此基础上完成锚链接预测.
总结与展望
1. 更多的结构和属性(More Structures and Properties)
- 尽管现有的结构和属性保留的网络嵌入方法提出了各种各样的结构和属性, 但是仍有些比较特别的网络结构没有被考虑比如高阶结构之一的网络 motifs. 此外, 传统的假设认为两个节点如果存在边连接, 那么这两个节点的表示会相似, 这样的假设对于中心节点信息的保留是无效的. 幂律定律告诉我们网络中的大部分节点存在很少的边连接, 如何通过有限的信息学习出这些信息较少的节点表示悬而未决.
2. 辅助信息的影响(The Effect of Side Information)
- 大部分使用辅助信息的网络嵌入算法都假设辅助信息和网络结构之间存在联系, 然而这种假设的正确性有多大是未知的, 在某写情况下辅助信息反而会降低嵌入性能. 如果能够探索出辅助信息和网络结构之间的互补性 (complementarity) 可能会十分有趣.在异质网络中, 元路径被广泛采用, 而元结构(meta structure, Huang et al. 2016)一种有向循环图结构则提供了另一种高阶结构信息, 可能会对异质网络嵌入性能提高具有积极作用.
3. 更多的高级信息和任务(More Advanced Information and Tasks)
- 通常来说, 网络嵌入算法都是针对通用问题设计, 如 link prediction和 node classification问题缺乏对特定应用的针对性, 如何探索网络嵌入使之可以解决更多问题是一个十分重要的研究方向. 如社交网络中的谣言检测(Mohapatra, and Abdelzaher 2012; Zhang et al.2015), 不同的领域有着各自的专业知识, 如何对它们进行建模整合到网络嵌入中具有挑战性.