Last updated on 2019-10-4…
#include <bits/stdc++.h>
using namespace std;
常用技巧整理
字符串
- 查找表:标记字符最新的位置 int table[256]={0}; table[s[i]] = i;
- 标记各单词中字符出现位置 vector<vector
> pos(128) - 滑动窗口 if(i>=l1) c2[s2[i-l1]-‘a’]–; memcmp(c1,c2,sizeof(c1);
- 反转字符串(左闭右开)reverse(s.begin(), s.end())
- 对撞指针int left = 0, right = s.size()-1
- 分词stringstream ss(str); while(getline(ss,word,’ ‘)){}
- 计数unordered_map<char,int>
- 去标点unordered_set
punctuations = {'!','?',',','\',';','.'}
数 组
- ij前后指针
- index对应位置存计数
- 给元素值赋正负来表达额外信息、index=INT_MIN
排 序
链 表 summary
二叉树 summary
- 递归(root->left, root->right)
- max(递归(root->left),递归(root->right))
- dfs(root)+递归(root->left)+递归(root->right)
矩 阵 summary
- 螺旋矩阵:环数 = min(m, n)/2
- 迷宫矩阵:path_temp.push_back({i,j});
- 生命游戏:状态压缩+二进制技巧 board[i][j] |= 0b10; board[i][j] »= 1;
- 最大路径和:best[i+1][j+1] = max(best[i+1][j] + a[i][j], best[i][j+1] + a[i][j]);
动态规划 summary1、summary
- 一维:单调栈(stack)
- 二维:编辑距离(下删/右插/右下替换) dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]})+1;
空间优化
- 将原值赋正负表达额外信息
- 二进制展开(不同位标识不同信息)
- 状态值用二进制标识,用位移作状态转移
常用宏定义
#define pb push_back
#define mp make_pair
#define PI acos(-1)
#define fi first
#define se second
#define INF 0x3f3f3f3f
#define INF64 0x3f3f3f3f3f3f3f3f
#define random(a,b) ((a)+rand()%((b)-(a)+1))
#define ms(x,v) memset((x),(v),sizeof(x))
#define scint(x) scanf("%d",&x );
#define scf(x) scanf("%lf",&x );
#define eps 1e-8
#define dcmp(x) (fabs(x) < eps? 0:((x) <0?-1:1))
using namespace std;
typedef long long LL;
typedef long double DB;
typedef pair<int,int> Pair;
const int maxn = 2e3+10;
const int MAX_V= 500+10;
const int MOD = 998244353;
边界值 limits.h
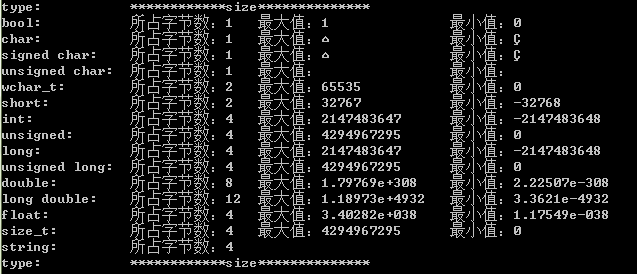
- 最严重的上溢是INT_MAX + INT_MAX :结果是-2
- 最轻微的上溢是INT_MAX + 1:结果是 INT_MIN
- 最轻微的下溢是INT_MIN - 1:结果是是INT_MAX
- 最严重的下溢是INT_MIN + INT_MIN:结果是0
其他:LLONG_MIN与LLONG_MAX,FLT_MIN与FLT_MAX,DBL_MIN与DBL_MAX
数值库 numeric
累加与递增填充
#include <numeric>
vector<int> vec(100, 1);
int sum = accumulate(vec.begin() , vec.end() , 0); //累加(第三个形参是累加的初值,这里置为0)
vector<char> vch(26);
iota(vch.begin(), vch.end(), 'a'); //递增填充
算法库 algorithm
比较
min(a, b); //返回a与b的较小者
max(a, b); //返回a与b的较大者
min({a, b, c}); //返回a、b、c的较小者
max({a, b, c}); //返回a、b、c的较大者
swap(a, b); //交换a与b的值,无返回值
int a[n]; //n必须是具体值
int minx = *(min_element(a,a+n));//返回数组的最小值
int maxx = *(max_element(a,a+n));//返回数组的最大值
//返回最小值的下标
vector<int> res;
vector<int>::iterator result = min_element(res.begin(), res.end());
int dis = distance(res.begin(), result);
lower_bound(dp.begin(), dp.end(), num); //返回 dp数组中 第一个大于等于 num的元素所在的位置
upper_bound(dp.begin(), dp.end(), num); //返回 dp数组中 第一个大于 num的元素所在的位置
find查找
//返回指向首个满足条件的迭代器,或若找不到这种元素则为last
vector<int> v{0, 1, 2, 3, 4};
int n = 3;
auto result = find(begin(v), end(v), n);
if (result != end(v)) cout<<"yes";
sort排序
//以升序排序范围[first, last)中的元素,不保证维持相等元素的顺序
sort(v.begin(), v.end());
//用lambda表达式排序,此处给了降序的例子
sort(v.begin(), v.end(), [](int a, int b) {
return b < a;
});
//自定义比较函数
bool cmp(const student& a,const student& b){
if(a.score<b.score)
return true;
return false;
}
sort(v.begin(), v.end(), cmp);
容器库
vector封装数组,list封装了链表,map和set封装了二叉树等
» c++ list, vector, map, set 区别与用法比较
关联 Map
为了实现快速查找,map内部本身就是按序存储的(比如红黑树)。 在我们插入<key, value>键值对时,就会按照key的大小顺序进行存储。根据key值快速查找记录,查找的复杂度基本是Log(N)。
#include <map>
unordered_map<char, int> mp = { //因为这段未用到map自动排序功能,所以unordered_map就行
{'a', 1},
{'b', 2},
{'c', 3}
};
char c; int sum = 0;
if (mp.count(c)){ //count函数:返回拥有关键 key 的元素数(更常用)
sum += mp.find(c)->second; //find函数:按key查找,返回的是指针
//若没找到则返回end();也可写成(*mp.find(c)).second
//其他:
map<char,int> m1; //默认从小到大排序
map<char,int, less<char>> m1; //从小到大
map<char,int,greater<char>> m1; //从大到小
m1.insert ( pair<char,int>('c',30) ); //插入,这里pair<.,.>()也可以用make_pair()
关联容器对比:(在前面加unordered_则变为非关联容器,按照键生成散列)
- set:唯一键的集合,按照键排序
- map:键值对的集合,按照键排序,键是唯一的
- multiset:键的集合,按照键排序
- multimap:键值对的集合,按照键排序
集合 set
在set中每个元素的值都唯一,而且系统能根据元素的值自动进行排序。应该注意的是set中数元素的值不能直接被改变。
#include <set>
set<int> s;
s.insert(1); //插入值
s.count(1); //返回出现次数
s.erase(s.begin()); //删除
s.erase(first,second); //范围删除,这里的first、second都是指针
auto pr = s.equal_range(3); //返回类型是pair<set<int>::const_iterator,set<int>::const_iterator>
cout<<"第一个大于等于 3 的数是 :"<<*pr.first<<endl;
cout<<"第一个大于 3 的数是 :"<<*pr.second<<endl;
s.insert(number).second //返回布尔值,表示是否插入成功,如果set里已有该number则失败
向量 vector
顺序容器,支持下标访问(V[i])
vector<int> v = {7, 5, 16, 8};
v.push_back(25); //加到末尾
v.pop_back(); //移除末尾
vec.insert(v.begin(), 15); //在指定位置添加元素,这里示例在开头添加元素15
v.clear(); //全部清除
v.erase(v.begin()); //移除位于 pos 的元素
v.erase(v.begin()+2, v.begin()+5); //移除范围 [first; last) 中的元素。
for(int n : v) //遍历
std::cout << n << '\n';
vector<int> table(256, -1); //生成256大小、初始值-1的一维数组
vector<vector<int> > dp(m + 1, vector<int>(n + 1, 0)); //创建m行n列的矩阵,初始化为0
//vector去重
auto it = unique(v.begin(),v.end());
v.erase(it,v.end());
队列 queue
一种FIFO(先进先出)数据结构(»另:优先队列)

queue<int> q; //普通的先进先出队列
q.size(); //返回q里元素个数
q.empty(); //返回q是否为空,空则返回true,否则返回false
q.push(k); //在q的末尾插入k
q.pop(); //删掉q的第一个元素
q.top(); //返回q的第一个元素
q.back(); //返回q的末尾元素
priority_queue<int> q1; //优先队列,默认大顶堆(less<int>)
priority_queue<int, vector<int>, less<int> > q1; //top+pop出来:14 12 10 8 6 大到小
priority_queue<int, vector<int>, greater<int> > q2; //top+pop出来:6 8 10 12 14 小到大
//形参依次为数据类型、保存数据的容器、元素比较方式
栈 stack
一种FILO(先进后出)数据结构

stack<int> s;
s.size(); //返回s里元素个数
s.empty(); //返回s是否为空,空则返回true,否则返回false
s.push(1); //入栈(向栈顶插入元素)
int a = s.top(); //访问栈顶的元素
s.pop(); //出栈(删除栈顶的元素)
字符串 cctype string cstring
cctype头文件 判别字符
#include <cctype>
char s;
s = tolower(s);//转为小写
s = toupper(s);//转为大写
//bool isxx(s):
isalnum //是否为字母或数字
isalpha //是否为字母
isdigit //是否为数字
ispunct //是否为标点符
islower //是否为小写字符
isupper //是否为大写字符
string头文件 基础操作
#include<string> //列出如下常用函数
for (auto it = s.begin(); it != s.end(); ++it) //begin指向首字符,end指向末尾'\n'
*it = toupper(*it);
str.empty(); //判断是否为空,即是否 begin() == end(),返回布尔值
str.insert(int p0, const char *s); //在p0位置插入字符串s
str.insert(int p0, const char *s, int n); //在p0位置插入字符串s的前n个字符
str.erase(iterator pos); //删除pos处的一个字符
str.erase(iterator pos, int n); //删除从pos开始的n个字符,比如erase(0,1)就是删除第一个字符
str.erase(iterator first, iterator last); //删除从first到last之间的字符
str.clear(); //如同通过执行 erase(begin(), end()),移除所有字符
int find(char c, int pos = 0); //从pos开始查找字符c在当前字符串的位置(注:从后往前查找用rfind)
int find(const char *s, int pos= 0); //从pos开始查找字符串s在当前串中的位置
str.replace(iterator first, iterator last, const char *s);//把[first,last)之间的部分替换为字符串s
str1 = str.substr(i); //返回str[i]位置以及之后的子串
str2 = str.substr(pos,n); //返回从pos开始的n个字符,包含pos的字符
类型转换
//#1、# 其他类型转为String
str = to_string(i); //这里的i可以为int、long long、float、double等
//但是char转string比较特殊:
str = string(1,c);
//#2、# String转为其他类型
s = "123.257";
//string --> int;
cout << stoi(s) << endl; //123
//string --> long
cout << stol(s) << endl; //123
//string --> float
cout << stof(s) << endl; //123.257
//string --> doubel
cout << stod(s) << endl; //123.257
cstring头文件 进阶操作
#include<cstring> //列出如下常用函数原型
int strcmp( const char *lhs, const char *rhs ); //实际原理是*lhs和*rhs字典值相减
char* strcpy( char* dest, const char* src ); //将后者复制给前者
char* strcat( char* dest, const char* src ); //将后者放在前者尾部,并返回前者
char* strchr( char* str, int ch ); //在str所指向的字节字符串中寻找字符ch的首次出现。认为终止空字符是字符串的一部分,而且若搜索 '\0' 则能找到它。
char* strstr( char* str, const char* target ); //在str所指的字节字符串中寻找字节字符串 target 的首次出现。不比较空终止字符。
正则表达式 regex
regex_match:匹配整个字符序列
regex re("\\d{3}-\\d{8}|\\d{4}-\\d{7}"); // fixed telephone
vector<string> str{ "010-12345678", "0319-9876543", "021-123456789"};
bool ret = regex_match(str, re);
regex_search:匹配字符子序列
string pattern{ "http|https://\\w*$" }; // fixed url
regex re(pattern);
vector<string> str{ "http://blog.csdn.net/fengbingchun", "https://github.com/fengbingchun",
"abcd://124.456", "abcd https://github.com/fengbingchun 123" };
bool ret = regex_search(str, re);
regex_replace:匹配整个并都替换
string pattern{ "\\d{18}|\\d{17}X" }; // fixed id card
regex re(pattern);
vector<std::string> str{ "123456789012345678", "abcd123456789012345678efgh","abcdefbg", "12345678901234567X" };
string fmt{ "********" };
string ret = std::regex_replace(str, re, fmt);
常用的元字符:
“^”:匹配输入字符串的开始位置,不匹配任何字符,要匹配”^”字符本身,需使用”\^”;
“$”:匹配输入字符串的结尾位置,不匹配任何字符,要匹配”$”字符本身,需使用”\$”;
“|”:将两个匹配条件进行逻辑"或"(Or)运算,如正则表达式”(him|her);
“*”: 零次或多次匹配前面的字符或子表达式,”*”等效于”{0,}”,如”\^*b”可以匹配”b”、”^b”、”^^b”、…;
“+”: 一次或多次匹配前面的字符或子表达式,等效于”{1,}”,如”a+b”可以匹配”ab”、”aab”、”aaab”、…;
“?”: 零次或一次匹配前面的字符或子表达式,等效于”{0,1}”,如”a[cd]?”可以匹配”a”、”ac”、”ad”;
“\”: 将下一字符标记为特殊字符、文本、反向引用或八进制转义符,如,”n”匹配字符”n”,”\n”匹配换行符,序列”\\”匹配”\”,”\(“匹配”(“;
“\w”:匹配字母或数字或下划线;“\W”:匹配任意不是字母、数字、下划线的字符;
“\s”:匹配任意的空白符,包括空格、制表符、换页符等空白字符的其中任意一个,与”[ \f\n\r\t\v]”等效;“\S”:同理相反
“\d”:匹配数字,任意一个数字,0~9中的任意一个,等效于”[0-9]”;“\D”:匹配任意非数字的字符,等效于”[^0-9]”;
“\b”: 匹配一个字边界,即字与空格间的位置,也就是单词和空格之间的位置,不匹配任何字符,如,"er\b"匹配"never"中的"er",但不匹配"verb"中的"er";“\B”非字边界匹配,"er\B"匹配"verb"中的"er",但不匹配"never"中的"er";
“\f”:匹配一个换页符,等价于”\x0c”和”\cL”;
“\n”:匹配一个换行符,等价于”\x0a”和”\cJ”;
“\r”:匹配一个回车符,等价于”\x0d”和”\cM”;
“\t”:匹配一个制表符,等价于”\x09”和”\cI”;
“\v”:匹配一个垂直制表符,等价于”\x0b”和”\cK”;
“\cx”:匹配”x”指示的控制字符,如,\cM匹配Control-M或回车符,”x”的值必须在”A-Z”或”a-z”之间,如果不是这样,则假定c就是"c"字符本身;
“{n}”:”n”是非负整数,正好匹配n次,如,"o{2}"与"Bob"中的"o"不匹配,但与"food"中的两个"o"匹配;
“{n,}”:”n”是非负整数,至少匹配n次,如,"o{2,}"不匹配"Bob"中的"o",而匹配"foooood"中的所有”o”,"o{1,}"等效于"o+","o{0,}"等效于"o*";
“{n,m}”:”n”和”m”是非负整数,其中n<=m,匹配至少n次,至多m次,如,"o{1,3}"匹配"fooooood"中的头三个o,'o{0,1}'等效于'o?',注意,不能将空格插入逗号和数字之间;如”ba{1,3}”可以匹配”ba”或”baa”或”baaa”;
“x|y”:匹配”x”或”y”,如,”z|food”匹配"z"或"food";”(z|f)ood”匹配"zood"或"food";
“[xyz]”:字符集,匹配包含的任一字符,如,"[abc]"匹配"plain"中的"a";
“[^xyz]”:反向字符集,匹配未包含的任何字符,匹配除了”xyz”以外的任意字符,如,"[^abc]"匹配"plain"中的"p";
“[a-z]”:字符范围,匹配指定范围内的任何字符,如,"[a-z]"匹配"a"到"z"范围内的任何小写字母;
“[^a-z]”:反向范围字符,匹配不在指定的范围内的任何字符,如,"[^a-z]"匹配任何不在"a"到"z"范围内的任何字符;
“( )”:将”(“和”)”之间的表达式定义为”组”group,并且将匹配这个表达式的字符保存到一个临时区域,一个正则表达式中最多可以保存9个,它们可以用”\1”到”\9”的符号来引用;
“(pattern)”:匹配pattern并捕获该匹配的子表达式,可以使用$0…$9属性从结果”匹配”集合中检索捕获的匹配;
“(?:pattern)”:匹配pattern但不捕获该匹配的子表达式,即它是一个非捕获匹配,不存储供以后使用的匹配,这对于用”or”字符” (|)”组合模式部件的情况很有用, 如,”industr(?:y|ies)”是比”industry|industries”更简略的表达式;
“(?=pattern)”: 非获取匹配,正向肯定预查,在任何匹配pattern的字符串开始处匹配查找字符串,该匹配不需要获取供以后使用。如,"Windows(?=95|98|NT|2000)"能匹配"Windows2000"中的"Windows",但不能匹配"Windows3.1"中的"Windows"。预查不消耗字符,也就是说,在一个匹配发生后,在最后一次匹配之后立即开始下一次匹配的搜索,而不是从包含预查的字符之后开始;
“(?!pattern)”: 非获取匹配,正向否定预查,在任何不匹配pattern的字符串开始处匹配查找字符串,该匹配不需要获取供以后使用。如"Windows(?!95|98|NT|2000)"能匹配"Windows3.1"中的"Windows",但不能匹配"Windows2000"中的"Windows";
要匹配某些特殊字符,需在此特殊字符前面加上”\”:
如要匹配字符”^”、”$”、”()”、”[]”、”{}”、”.”、”?”、”+”、”*”、”|”,需使用” \^”、” \$”、” \ (“、”\)”、” \ [“、”\]”、” \{“、”\}”、” \.”、” \?”、” \+”、” \*”、” \|”。
经典题目
字符的最短距离
【题干】给定一个字符串 S 和一个字符 C。返回一个代表字符串 S 中每个字符到字符串 S 中的字符 C 的最短距离的数组。
- 输入: S = “loveleetcode”, C = ‘e’
- 输出: [3, 2, 1, 0, 1, 0, 0, 1, 2, 2, 1, 0]
class Solution {
public:
//第一步,先假设在很远的位置有个C字符,那么从左到右开始遍历,找出每个字符到其最近的左边的字符C的距离;
//第二步,先假设在很远的位置有个C字符,那么从右到左开始遍历,找出每个字符到其最近的右边的字符C的距离,并和第一步求出的距离进行比较,找出最小值为结果;
vector<int> shortestToChar(string S, char C) {
int len = S.size();
vector<int> ans(len,0);
int index = -10000;
for(int i=0;i<len;i++){
if(S[i]==C)
index = i;
ans[i] = abs(i-index);
}
//此时ans为[10000, 10001, 10002, 0, 1, 0, 0, 1, 2, 3, 4, 0]
index = -10000;
for(int i=len-1;i>=0;i--){
if(S[i]==C)
index = i;
ans[i] = min(abs(i-index), ans[i]);
}
//此时ans为[3, 2, 1, 0, 1, 0, 0, 1, 2, 2, 1, 0]
return ans;
}
};
匹配子序列的单词数
【题干】给定字符串 S 和单词字典 words, 求 words[i] 中是 S 的子序列的单词个数。
输入: S = “abcde” words = [“a”, “bb”, “acd”, “ace”] 输出: 3
解释: 有三个是 S 的子序列的单词: “a”, “acd”, “ace”。
class Solution {
private:
unordered_map<string, bool> mp;
bool isMatch(const string& word, const vector<vector<int>>& pos){
if(mp.count(word)) return mp[word];
int last_index = -1;
for(char c :word){
vector<int> p = pos[c]; //取出这个字符的出现序列
auto it = lower_bound(p.begin(),p.end(),last_index+1); //lower_bound返回一个迭代器,指向键值>= key的第一个元素。
if(it == p.end())
return mp[word] = false;
last_index = *it;
}
return mp[word] = true;
}
public:
int numMatchingSubseq(string S, vector<string>& words) {
vector<vector<int>> pos(128); //第一维是字符对应的ascii数值,第二维是其出现位置的int序列
for(int i=0; i<S.length(); ++i)
pos[S[i]].push_back(i);
int ans = 0;
for(string word : words)
ans += isMatch(word, pos);
return ans;
}
};
消失的数字
【题干】给一个长度为n的数组,这个数组里面包含1-n的数字,数字的分布并不均匀,数字可以出现0-n次。所以这个数组中可能并不完全包含1-n中的所有数字
现在需要你在常数时间和不用额外空间的情况下找出那些数字没有出现过
解题思想是遍历两轮:
- 第一轮将每个数字对应的那个位置的数字变成负值(因为所有数都是正的,这么做不影响后续)
- 第二轮,统计那些没有变成负值的,这些就是没有出现过的数
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int> &nums) {
for (auto num : nums) {
int index = num > 0 ? num : -num;
index--;
if (nums[index] > 0) {
nums[index] = -nums[index];
}
}
vector<int> result;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > 0) {
result.push_back(i + 1);
}
}
return result;
}
};
环形链表II
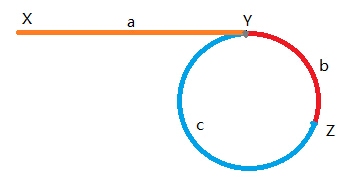
【题干】给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
串长a + n,其中n为循环,当a + b步的慢指针与快指针相遇时,快指针已经走过了k圈。
即a + b + k * n = 2 * (a+b),求a,得到a = k * n - b。
也就是X走a步,等于Z位置上的指针再走k圈,相遇于Y点。
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *p = head, *q = head;
while (q && q->next) {
p = p->next;
q = q->next->next;
if (p == q) {
while (head != q) {
q = q->next;
head = head->next;
}
return head;
}
}
return NULL;
}
};
路径总和III
【题干】给定一个二叉树,它的每个结点都存放着一个整数值。
- 找出路径和等于给定数值的路径总数
- 路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)
- 二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数
class Solution {
public:
int dfs(TreeNode* root, int sum){
if(!root) return 0;
int res = 0;
if(root->val == sum)
res += 1;
res += dfs(root->left, sum - root->val);
res += dfs(root->right, sum - root->val);
return res;
}
int pathSum(TreeNode* root, int sum) {
if(!root) return 0;
return dfs(root, sum) + pathSum(root->left, sum) + pathSum(root->right, sum);
}
};
模拟行走机器人
【题干】机器人在一个无限大小的网格上行走,从点 (0, 0) 处开始出发,面向北方。该机器人可以接收以下三种类型的命令:
- -2:向左转 90 度
- -1:向右转 90 度
- 1 <= x <= 9:向前移动 x 个单位长度
在网格上有一些格子被视为障碍物。第 i 个障碍物位于网格点 (obstacles[i][0], obstacles[i][1])。如果机器人试图走到障碍物上方,那么它将停留在障碍物的前一个网格方块上,但仍然可以继续该路线的其余部分。
返回从原点到机器人的最大欧式距离的平方。
示例:commands = [4,-1,4,-2,4], obstacles = [[2,4]] 输出: 65 解释: 机器人在左转走到 (1, 8) 之前将被困在 (1, 4) 处
class Solution {
public:
int robotSim(vector<int>& commands, vector<vector<int>>& obstacles) {
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
int x = 0, y = 0, di = 0;
unordered_set<pair<int, int>> obstacleSet;
for (vector<int> obstacle: obstacles)
obstacleSet.insert(make_pair(obstacle[0], obstacle[1]));
int ans = 0;
for (int cmd: commands) {
if (cmd == -2)
di = (di + 3) % 4;
else if (cmd == -1)
di = (di + 1) % 4;
else {
for (int k = 0; k < cmd; ++k) {
int nx = x + dx[di];
int ny = y + dy[di];
if (obstacleSet.find(make_pair(nx, ny)) == obstacleSet.end()) {
x = nx;
y = ny;
ans = max(ans, x*x + y*y);
}
}
}
}
return ans;
}
};
螺旋矩阵
【题干】给定一个包含 m x n 个元素的矩阵(m 行, n 列),请按照顺时针螺旋顺序,返回矩阵中的所有元素。
这道题让我们将一个矩阵按照螺旋顺序打印出来,我们只能一条边一条边的打印。
首先我们要从给定的mxn的矩阵中算出按螺旋顺序有几个环,注意最终间的环可以是一个数字,也可以是一行或者一列。
环数的计算公式是min(m, n) / 2,知道了环数,我们可以对每个环的边按顺序打印
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
if (matrix.empty() || matrix[0].empty()) return res;
int m = matrix.size(), n = matrix[0].size();
int c = m > n ? (n + 1) / 2 : (m + 1) / 2;
int p = m, q = n;
for (int i = 0; i < c; ++i, p -= 2, q -= 2) {
for (int col = i; col < i + q; ++col)
res.push_back(matrix[i][col]);
for (int row = i + 1; row < i + p; ++row)
res.push_back(matrix[row][i + q - 1]);
if (p == 1 || q == 1) break;
for (int col = i + q - 2; col >= i; --col)
res.push_back(matrix[i + p - 1][col]);
for (int row = i + p - 2; row > i; --row)
res.push_back(matrix[row][i]);
}
return res;
}
};
生命游戏
【题干】见Leetcode 289,遵从4条生存规律的细胞存活问题
class Solution {
//当前状态为二进制的最后一位,下一状态存放在倒数第二位,等全部更新完第二位后,一起右移一位即可,空间复杂度就降为O(1)了
public:
void gameOfLife(vector<vector<int>>& board) {
int m = board.size();
int n = m? board[0].size() : 0;
for(int i=0; i<m ;i++){
for(int j=0; j<n ; j++){
int lives = 0;
for(int y=max(0,i-1); y<min(m,i+2); y++)
for(int x=max(0,j-1); x<min(n,j+2); x++)
lives += board[y][x] & 1;
if(lives==3 || lives-board[i][j]==3)
board[i][j] |= 0b10;
}
}
for(int i=0; i<m; i++)
for(int j=0; j<n; j++)
board[i][j] >>= 1;
}
};
编辑距离
【题干】见Leetcode 72,给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 (插入、删除、替换)。
class Solution {
public:
int minDistance(string word1, string word2) {
//定义 dp[i][j] := 将 word1[0:i] 转换为 word2[0:j] 的操作数,
//向下走一步 代表 删除一个字符
//向右走一步 代表 插入一个字符
//斜着右下走一步 代表 替换一个字符
int m = word1.size();
int n = word2.size();
vector<vector<int> > dp(m + 1, vector<int>(n + 1));;
//初始化
dp[0][0] = 0;
for(int i = 1; i <= m; i++)
dp[i][0] = i;
for(int j = 1; j <= n; j++)
dp[0][j] = j;
for(int i = 1; i <= m; i++){
for(int j = 1; j <= n; j++){
if(word1[i-1] == word2[j-1])
dp[i][j] = dp[i-1][j-1];
else
dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]})+1;
}
}
return dp[m][n];
}
};
位运算
【题干】求两个整数之间的汉明距离:这两个数字对应二进制位不同的位置的数目。
class Solution {
public:
int hammingDistance(int x, int y) {
int res = 0, exc = x ^ y;
for (int i = 0; i < 32; ++i) {
res += (exc >> i) & 1;
}
return res;
}
};
【题干】给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
class Solution {
public:
int singleNumber(vector<int>& nums) {
int result = nums[0];
for(int i = 1; i < nums.size(); i++){
result = result ^ nums[i];
}
return result;
}
};
【题干】给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。
对每个整数以32位表示,分别统计每一位上1的个数,最后该位数上的和对3取余数; 如果余数不为0,则说明该位上只出现一次的元素,在该位上有1; 通过移位操作和1做位与运算,则可求得当前元素在该位是否有1。
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ret = 0;
for(int i=0; i<32; ++i){
int sum = 0;
for(int j=0; j<nums.size(); ++j){
sum += (nums[j]>>i) & 1;
}
ret |= (sum % 3)<<i;
}
return ret;
}
};
【题干】 见leetcode 289,是一道矩阵状态同步更新的题。
技巧:当前状态为二进制的最后一位,下一状态存放在倒数第二位,等全部更新完第二位后,一起右移一位即可,空间复杂度就降为O(1)了
class Solution {
public:
void gameOfLife(vector<vector<int>>& board) {
int m = board.size();
int n = m? board[0].size() : 0;
for(int i=0; i<m ;i++){
for(int j=0; j<n ; j++){
int lives = 0;
for(int y=max(0,i-1); y<min(m,i+2); y++) //判定边界的技巧
for(int x=max(0,j-1); x<min(n,j+2); x++)
lives += board[y][x] & 1;
if(lives==3 || lives-board[i][j]==3) //更新二进制的倒数第二位
board[i][j] |= 0b10;
}
}
for(int i=0; i<m; i++)
for(int j=0; j<n; j++)
board[i][j] >>= 1;
}
};
【题干】下一个更大元素 II:给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
int n = nums.size();
vector<int> next(n,-1);
stack<int> s;
for (int i = 0; i < n * 2; i++) { //解决数组循环了
int num = nums[i % n];
while (!s.empty() && nums[s.top()] < num){
next[s.top()] = num;
s.pop();
}
if (i < n) s.push(i);
}
return next;
}
};
【题干】只出现一次的数字III:给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。
思路:先全部异或一次, 得到的结果, 考察其的某个非0位(比如最高非0位), 那么只出现一次的两个数中, 在这个位上一个为0, 一个为1, 由此可以将数组中的元素分成两部分,重新遍历, 求两个异或值
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
vector<int> res(2, 0);
int num = 0, index = 0;
for (int n : nums)
num ^= n;
while ((num & 1) == 0) {
num >>= 1;
index++;
}
for (int n : nums) {
if ((n >> index) & 1)
res[0] ^= n;
else
res[1] ^= n;
}
return res;
}
};