C++二叉树

#include <iostream>
#include <string>
#include <queue>
#include <stack>
using namespace std;

string str;
int i;

struct TreeNode{
	char val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(char x) : val(x), left(NULL), right(NULL) {}
};

TreeNode* createTree(){
	char c = str[i++];
	if(c =='#') return NULL;
	TreeNode *root = new TreeNode(c);
	root->left  = createTree();
	root->right = createTree();
	return root;
}

int main(){
	str = "AB#C##D##";
	i = 0;
	TreeNode *root = createTree();
	Visit(root); 
	cout<<endl;
	return 0;
}

void preVisit(TreeNode *root){
	if(!root) return;
	cout<< root->val << " ";
	preVisit(root->left);
	preVisit(root->right);
}

void midVisit(TreeNode *root){
	if(!root) return;
	midVisit(root->left);
	cout<< root->val << " ";
	midVisit(root->right);
}

void postVisit(TreeNode *root){
	if(!root) return;
	postVisit(root->left);
	postVisit(root->right);
	cout<< root->val << " ";
}

void preVisit2(TreeNode *root){
	if(!root) return;
	TreeNode *p = root;
	stack<TreeNode *> s;
	while(p || !s.empty()){
		if(p){
			cout<< p->val << " ";
			s.push(p);
			p = p->left;
		}
		else{
			p = s.top();
			s.pop();
			p = p->right;
		}
	}
}

void midVisit2(TreeNode *root){
	if(!root) return;
	TreeNode *p = root;
	stack<TreeNode *> s;
	while(p || !s.empty()){
		if(p){
			s.push(p);
			p = p->left;
		}
		else{
			p = s.top();
			cout<< p->val << " ";
			s.pop();
			p = p->right;
		}
	}
}

void postVisit2(TreeNode *root){
    if(!root) return;
    stack<TreeNode *> s;
    TreeNode *cur;       //当前结点 
    TreeNode *pre=NULL;  //前一次访问的结点 
    s.push(root);
    while(!s.empty())
    {
        cur=s.top();
        if( (!cur->left && !cur->right) || (pre && (pre==cur->left||pre==cur->right)) ){
            cout<< cur->val << " ";  //如果当前结点没有孩子结点或者孩子节点都已被访问过 
            s.pop();
            pre=cur; 
        }
        else{
            if(cur->left ) s.push(cur->left );
            if(cur->right) s.push(cur->right);
        }
    }    
}

void hieVisit(TreeNode *root){
	if(!root) return;
	TreeNode *temp; //保存队列出队时的临时变量
	queue<TreeNode *> q;
	q.push(root);
	while(!q.empty()){
		temp = q.front();
		q.pop();
		cout<< temp->val << " ";
		if(temp->left ) q.push(temp->left);
		if(temp->right) q.push(temp->right);
	}
}

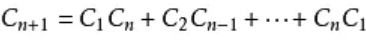
int numTrees(int n) {  
	vector<int> count(n+1, 0);  
	count[0] =1;  
	count[1] =1;  
	for(int i = 2; i <= n; i++){  
		for(int j = 0; j < i; j++){  
			count[i] += count[j]*count[i-j-1];   
		}  
	}  
	return count[n];  
}