Last updated on 2019-4-11…
Cost Function和Loss Function的区别：
- Cost Function：指基于参数w和b，在所有训练样本上的总成本
- Loss Function：指单个训练样本的损失函数
均方误差 MSE
假设是高斯分布，又名正态分布
均方误差的含义是求一个batch中n个样本的n个输出与期望输出的差的平方的平均值。
回归问题中常用的损失函数式均方误差(MSE,mean squared error)，定义如下：
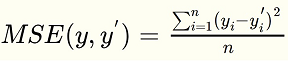
交叉熵 Cross Entropy
假设是伯努利分布，又名0-1分布。
分类问题中，预测结果是（或可以转化成）输入样本属于n个不同分类的对应概率。 比如对于一个4分类问题，期望输出应该为 p=[0,1,0,0]，实际输出为 q=[0.2,0.4,0.4,0]。 计算p与q之间的差异所使用的方法，就是损失函数，分类问题中常用损失函数是交叉熵。
从熵、KL散度到交叉熵
熵(Entropy) -> KL散度(Kullback-Leibler Divergence) -> 交叉熵 (Cross Entropy)
KL散度可以被用于计算代价，而在特定情况下最小化KL散度等价于最小化交叉熵。而交叉熵的运算更简单，所以用交叉熵来当做代价。
- 熵：可以表示一个事件A的自信息量，也就是A包含多少信息。
- KL散度：可以用来表示从事件A的角度来看，事件B有多大不同。
- 交叉熵：可以用来表示从事件A的角度来看，如何描述事件B。
ps：熵是度量样本集合纯度的最常用指标，代表一个系统中包含多少信息量，信息量越大表明系统的不确定性越大。
- 当样本类别均匀分布时，熵最大，纯度最小
- 当样本只有一个类别时，熵最小（=0），纯度最大
KL散度：
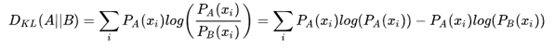
熵：
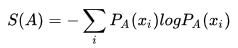
交叉熵：
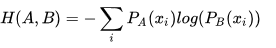
所以，A和B的交叉熵 = A与B的KL散度 - A的熵。
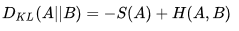
从对数损失到交叉熵
单样本对数损失：
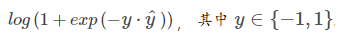
多样本对数损失：
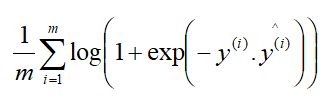
将sigmoid代入对数损失，于是得到了交叉熵。（»推导过程）
交叉熵描述的是两个概率分布之间的距离，距离越小表示这两个概率越相近，越大表示两个概率差异越大。对于两个概率分布 p 和 q ，使用 q 来表示 p 的交叉熵为：
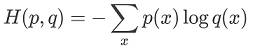
上式表示的物理意义是使用概率分布 q 来表示概率分布 p 的困难程度，q 是预测值，p 是期望值。
由公式可以看出来，p 与 q 之间的交叉熵 和 q 与 p 之间的交叉熵不是等价的。
神经网络的输出，也就是前向传播的输出可以通过Softmax变成概率分布，之后就可以使用交叉熵函数计算损失了。
逻辑回归中的交叉熵
- MSE的假设是高斯分布，交叉熵的假设是伯努利分布，而逻辑回归采用的就是伯努利分布
- MSE会导致代价函数J(θ)非凸，这会存在很多局部最优解，而我们更想要代价函数是凸函数
- MSE相对于交叉熵而言会加重梯度弥散（MSE的梯度是交叉熵梯度的1/4，当训练结果接近真实值时会因为梯度算子极小，MSE使得模型的收敛速度变得非常的缓慢。）
以上解释的参考链接：Poll的笔记
单样本交叉熵：
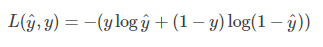
多样本交叉熵：
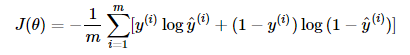
y代表期望输出（实际值），y带上标 代表模型实际输出（预测值）
其他常见损失函数
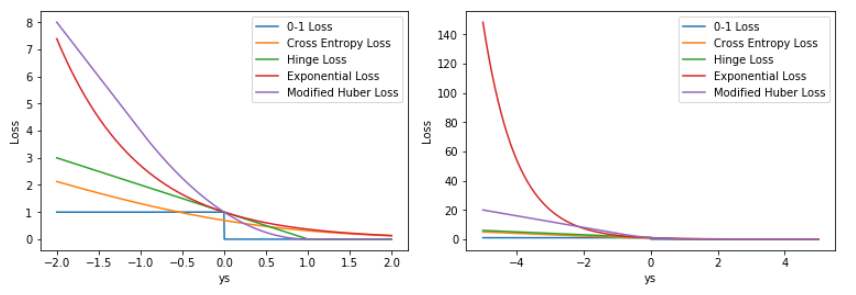
0-1损失函数
感知机模型采用
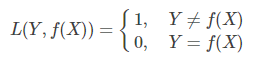
当预测错误时，损失函数值为1，预测正确时，损失函数值为0。
该损失函数不考虑预测值和真实值的误差程度，也就是只要预测错误，预测错误差一点和差很多是一样的。
但是由于相等这个条件太过严格，因此我们可以放宽条件，即满足差绝对值小于T时认为相等：
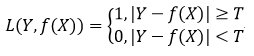
绝对值损失函数(absolute，MAE)
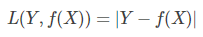MAE相对MSE来说，差距不会被平方放大。
对数损失函数(logarithmic)
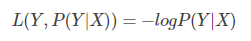
该损失函数用到了极大似然估计的思想。
P(Y|X)通俗的解释：在当前模型的基础上，对于样本X，其预测值为Y，也就是预测正确的概率。
由于概率之间的同时满足需要使用乘法，为了将其转化为加法，我们将其取对数。
最后由于是损失函数，所以预测正确的概率越高，其损失值应该是越小，因此再加个负号取个反。
指数损失函数(Exponential)
AdaBoost模型采用
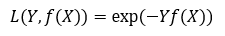
Hinge损失函数
SVM模型采用
Hinge loss用于最大间隔（maximum-margin）分类，其中最有代表性的就是支持向量机SVM。
标准形式：
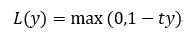其中，t为目标值（-1或+1），y是分类器输出的预测值，并不直接是类标签。
- 当t和y的符号相同时（表示y预测正确）并且|y|≥1时，hinge loss为0；
- 当t和y的符号相反时，hinge loss随着y的增大线性增大。
与上面统一的形式：
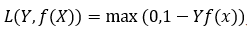
总结
