Last updated on 2019-10-4…
总览
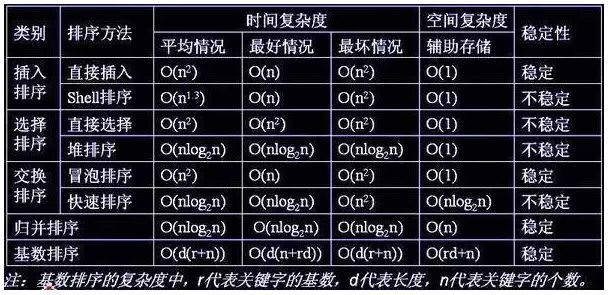
关于稳定性（简单说就是两个相等的元素，排序前后相对位置不变）
- 稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序；
- 不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。
冒泡排序
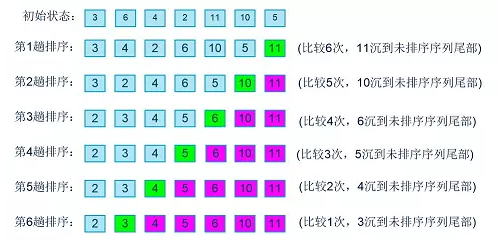
冒泡排序是最简单粗暴的排序方法之一。它的原理很简单，每次从左到右两两比较，把大的交换到后面，每次可以确保将前M个元素的最大值移动到最右边。
步骤
1.从左开始比较相邻的两个元素x和y，如果 x > y 就交换两者
2.执行比较和交换，直到到达数组的最后一个元素
3.重复执行1和2，直到执行n次，也就是n个最大元素都排到了最后
void bubble_sort(vector<int> &nums)
{
for (int i = 0; i < nums.size() - 1; i++) { // times
for (int j = 0; j < nums.size() - i - 1; j++) { // position
if (nums[j] > nums[j + 1]) {
int temp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = temp;
}
}
}
}
复杂度分析
由于我们要重复执行n次冒泡，每次冒泡要执行n次比较（实际是1到n的等差数列，也就是(a1 + an) * n / 2 ），也就是 O(n^2)。 空间复杂度是O(1)。
插入排序
插入排序的原理是从左到右，把选出的一个数和前面的数进行比较，找到最适合它的位置放入，使前面部分有序。
步骤
1.从左开始，选出当前位置的数x，和它之前的数y比较，如果x < y则交换两者
2.对x之前的数都执行1步骤，直到前面的数字都有序
3.选择有序部分后一个数字，插入到前面有序部分，直到没有数字可选择
void insert_sort(vector<int> &nums)
{
for (int i = 1; i < nums.size(); i++) { // position
for (int j = i; j > 0; j--) {
if (nums[j] < nums[j - 1]) {
int temp = nums[j];
nums[j] = nums[j - 1];
nums[j - 1] = temp;
}
}
}
}
复杂度分析
因为要选择n次，而且插入时最坏要比较n次，所以时间复杂度同样是O(n^2)。空间复杂度是O(1)。
归并排序
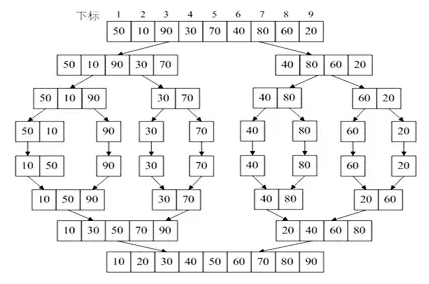
归并排序是采用分治法（Divide and Conquer）的一个典型例子。这个排序的特点是把一个数组打散成小数组，然后再把小数组拼凑再排序，直到最终数组有序。
步骤
1.把当前数组分化成n个单位为1的子数组，然后两两比较合并成单位为2的n/2个子数组
2.继续进行这个过程，按照2的倍数进行子数组的比较合并，直到最终数组有序
void merge_array(vector<int> &nums, int b, int m, int e, vector<int> &temp)
{
int lb = b, rb = m, tb = b;
while (lb != m && rb != e)
if (nums[lb] < nums[rb])
temp[tb++] = nums[lb++];
else
temp[tb++] = nums[rb++];
while (lb < m)
temp[tb++] = nums[lb++];
while (rb < e)
temp[tb++] = nums[rb++];
for (int i = b;i < e; i++)
nums[i] = temp[i];
}
void merge_sort(vector<int> &nums, int b, int e, vector<int> &temp)
{
int m = (b + e) / 2;
if (m != b) {
merge_sort(nums, b, m, temp);
merge_sort(nums, m, e, temp);
merge_array(nums, b, m, e, temp);
}
}
复杂度分析
在merge_array过程中，实际的操作是当前两个子数组的长度，即2m。又因为打散数组是二分的，最终循环执行数是logn。所以这个算法最终时间复杂度是O(nlogn)，空间复杂度是O(n)。
选择排序
选择排序的原理是，每次都从乱序数组中找到最大（最小）值，放到当前乱序数组头部，最终使数组有序。
步骤
1.从左开始，选择后面元素中最小值，和最左元素交换
2.从当前已交换位置往后执行，直到最后一个元素
void selection_sort(vector<int> &nums)
{
for (int i = 0; i < nums.size(); i++) { // position
int min = i;
for (int j = i + 1; j < nums.size(); j++) {
if (nums[j] < nums[min]) {
min = j;
}
}
int temp = nums[i];
nums[i] = nums[min];
nums[min] = temp;
}
}
复杂度分析
每次要找一遍最小值，最坏情况下找n次，这样的过程要执行n次，所以时间复杂度还是O(n^2)。空间复杂度是O(1)。
希尔排序
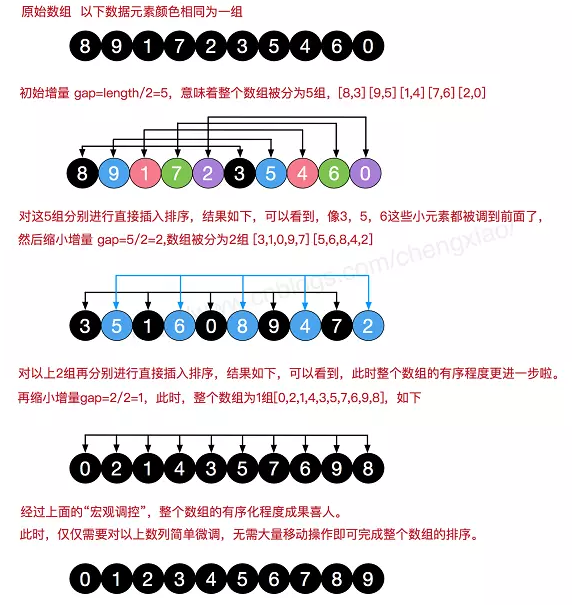
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
步骤
1.计算当前步长，按步长划分子数组
2.子数组内插入排序
3.步长除以2后继续1、2两步，直到步长最后变成1
void shell_sort(vector<int> &nums)
{
for (int gap = nums.size() >> 1; gap > 0; gap >>= 1) { // times
for (int i = gap; i < nums.size(); i++) { // position
int temp = nums[i];
int j = i - gap;
for (; j >= 0 && nums[j] > temp; j -= gap) {
nums[j + gap] = nums[j];
}
nums[j + gap] = temp;
}
}
}
复杂度分析
希尔排序的时间复杂度受步长的影响，具体分析在维基百科。
快速排序
快速排序也是利用分治法实现的一个排序算法。快速排序和归并排序不同，它不是一半一半的分子数组，而是选择一个基准数，把比这个数小的挪到左边，把比这个数大的移到右边。然后不断对左右两部分也执行相同步骤，直到整个数组有序。
步骤
1.用一个基准数将数组分成两个子数组
2.将大于基准数的移到右边，小于的移到左边
3.递归的对子数组重复执行1、2，直到整个数组有序
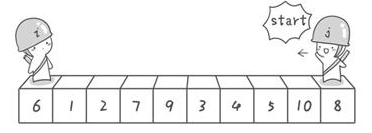
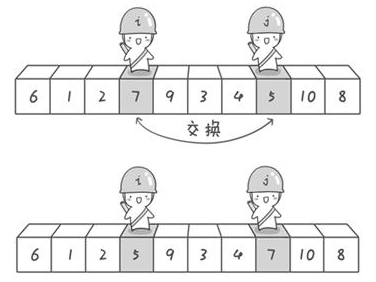详细图解见这篇文章
//快排的递归写法 qsort(nums,0,nums.size()-1);
void qsort(vector<int> &num, int begin, int end){
if(begin>=end) return;
int l = begin, r = end, x = num[l]; // 把最左边的数作为基数x
while(l<r){
while(l<r&&num[r]>x) --r; // 从右向左找第一个小于x的数
if(l<r)
num[l++] = num[r];
while(l<r&&num[l]<x) ++l; // 从左向右找第一个大于x的数
if(l<r)
num[r--] = num[l];
}
num[l] = x;
qsort(num,begin,l-1);
qsort(num,l+1,end);
}
//快排的非递归写法：用一个栈来保存左右边界下标，在栈弹空之前以栈顶两元素作为左右边界下标进行partition
void Push(stack<int>& st, int l, int r){
if(l>=r) return;
st.push(r);
st.push(l);
}
void qsort(vector<int>& nums, int begin, int end){
stack<int> st;
int left,right,x;
Push(st,begin,end);
while(!st.empty()){
left = st.top();
st.pop();
right = st.top();
st.pop();
int l = left, r = right;
x = nums[l];
while(l<r){
while(l<r&&nums[r]>=x) --r;
if(l<r) nums[l++] = nums[r];
while(l<r&&nums[l]<=x) ++l;
if(l<r) nums[r--] = nums[l];
}
nums[l] = x;
Push(st,left,l-1);
Push(st,l+1,right);
}
}
复杂度分析
快速排序也是一个不稳定排序，时间复杂度看维基百科。空间复杂度是O(nlogn)。
堆排序
堆排序经常用于求一个数组中最大k个元素时。因为堆实际上是一个完全二叉树，所以用它可以用一维数组来表示。因为最大堆的第一位总为当前堆中最大值，所以每次将最大值移除后，调整堆即可获得下一个最大值，通过一遍一遍执行这个过程就可以得到前k大元素，或者使堆有序。
在了解算法之前，首先了解在一维数组中节点的下标：
- i节点的父节点 parent(i) = floor((i-1)/2)
- i节点的左子节点 left(i) = 2i + 1
- i节点的右子节点 right(i) = 2i + 2
步骤
1.构造最大堆（Build Max Heap）：首先将当前元素放入最大堆下一个位置，然后将此元素依次和它的父节点比较，如果大于父节点就和父节点交换，直到比较到根节点。重复执行到最后一个元素。
2.最大堆调整（Max Heapify）：调整最大堆即将根节点移除后重新整理堆。整理方法为将根节点和最后一个节点交换，然后把堆看做n-1长度，将当前根节点逐步移动到其应该在的位置。
3.堆排序（HeapSort）：重复执行2，直到所有根节点都已移除。
void heap_sort(vector<int> &nums)
{
int n = nums.size();
for (int i = n / 2 - 1; i >= 0; i--) { // build max heap
max_heapify(nums, i, nums.size() - 1);
}
for (int i = n - 1; i > 0; i--) { // heap sort
int temp = nums[i];
num[i] = nums[0];
num[0] = temp;
max_heapify(nums, 0, i);
}
}
void max_heapify(vector<int> &nums, int beg, int end)
{
int curr = beg;
int child = curr * 2 + 1;
while (child < end) {
if (child + 1 < end && nums[child] < nums[child + 1]) {
child++;
}
if (nums[curr] < nums[child]) {
int temp = nums[curr];
nums[curr] = nums[child];
num[child] = temp;
curr = child;
child = 2 * curr + 1;
} else {
break;
}
}
}
复杂度分析
堆执行一次调整需要O(logn)的时间，在排序过程中需要遍历所有元素执行堆调整，所以最终时间复杂度是O(nlogn)。空间复杂度是O(1)。
基数排序
基数排序 (Radix Sort) 是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。
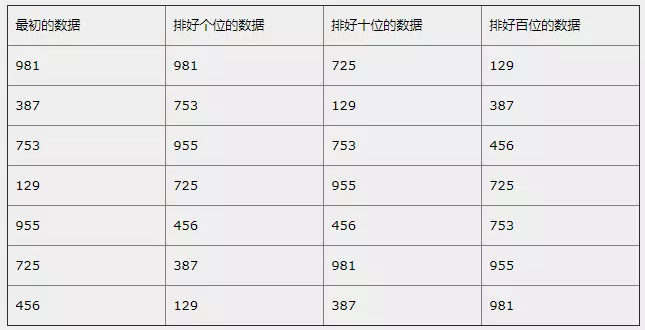
步骤
1.把所有元素都分配到相应的桶中
2.把所有桶中的元素都集合起来放回到数组中
3.依次循环上面两步，循环次数为最大元素最高位数
radix sort
- 基数排序也是基于一种假设，假设所有数都是非负的整数
- 基数排序的基本思路是从低位至高位依次比较每个数的对应位，并排序；对应位的比较采用计数排序也可以采用桶排序；
- 基数排序是一种稳定的排序方法，不稳定的话也没法排序，因为某一位相同并不代表两个数相同；
void countSort(vector<int> &nums,int exp){
vector<int> range(10,0);
int length=nums.size();
vector<int> tmpVec(length,0);
for(int i=0;i<length;++i)
range[(nums[i]/exp)%10]++;
for(int i=1;i<range.size();++i)
range[i]+=range[i-1];//统计本应该出现的位置
for(int i=length-1;i>=0;--i){
tmpVec[range[(nums[i]/exp)%10]-1]=nums[i];
range[(nums[i]/exp)%10]--;
}
nums=tmpVec;
}
void radixSort(vector<int> &nums){
int length=nums.size();
int max=-1;
for(int i=0;i<length;++i){ //提取出最大值
if(nums[i]>max)
max=nums[i];
}
//提取每一位并进行比较，位数不足的高位补0
for(int exp=1;max/exp>0;exp*=10)
countSort(nums,exp);
}
复杂度分析
- 通过上文可知，假设在基数排序中，r为基数，d为位数。则基数排序的时间复杂度为O(d(n+r))。我们可以看出，基数排序的效率和初始序列是否有序没有关联。
- 在基数排序过程中，对于任何位数上的基数进行“装桶”操作时，都需要n+r个临时空间。
- 在基数排序过程中，每次都是将当前位数上相同数值的元素统一“装桶”，并不需要交换位置。所以基数排序是稳定的算法。
第k大
借鉴快排
//调用示例： topk(nums,k,0,nums.size()-1)
int topk(vector<int> &nums,int k,int left,int right){
int l=left, r=right, x=nums[l], n=nums.size();
while(l<r){
while(l<r && nums[r]>x) r--;
if(l<r) nums[l++]=nums[r];
while(l<r && nums[l]<=x) l++;
if(l<r) nums[r--]=nums[l];
}
nums[l]=x;
if(l==n-k) return x;
else if(l<n-k) return topk(nums,k,l+1,right);
else return topk(nums,k,left,l-1);
}
利用最小堆
- 例如，假设有10个数，要求求第3大的数，第一步选取任意的3个数，比如说是前3个，将这3个数建成最小堆
- 然后从第4个数开始，与堆顶的数比较，如果比堆顶的数要小，那么这个数就不要
- 如果比堆顶的数大，则舍弃当前的堆顶而将这个数作为新的堆顶，并再去维护堆（向下调整，即不断与子节点中的较小者交换）
//利用multiset本身有序，维持multiset大小K，则multiset首元素即为所求.
//注意： 由于数组本身存在重复元素，所以这里要用multiset
int findKthLargest(vector<int>& nums, int k) {
multiset<int> s;
for(auto &m:nums){
s.insert(m);
if(s.size()>k) s.erase(s.begin());
}
return *s.begin();
}
STL库函数
nth_element(L,kth,R)
O(n)复杂度，使得[L,kth)的元素都比kth小，(kth,R)的元素都比kth大
原理类似快排：在当前区间[L,R]上，找一个基准位置mid。通过线性的扫描交换，使得[L,mid)的元素都比mid小，(mid,R)的元素都比mid大，此时mid上的元素就是第mid小的。然后判断k在哪半边，继续递归处理。
int findKthLargest(vector<int>& nums, int k) {
nth_element(nums.begin(),nums.end()-k,nums.end());
return *(nums.end()-k);
}
