PyTorch基础

Last updated on 2018-10-25…

PyTorch文档

PyTorch是Torch的python版本，早期Torch是基于Lua语言的。相比tensorflow来说，其底层更亲民一些，也更适合动态的网络。

下面代码转载自莫烦的课程，个人根据自己的理解做了一写改动跟注释。

numpy与tensor的转换

import torch
import numpy as np

np_data = np.arange(6).reshape((2, 3))   #numpy数组
torch_data = torch.from_numpy(np_data)   #numpy数组转tensor
tensor2array = torch_data.numpy()        #tensor转numpy数组

print(
    'numpy array:\n', np_data,          # [[0 1 2], [3 4 5]]
    'torch tensor:\n', torch_data,      #   0 1 2 \n 3 4 5    [torch.LongTensor of size 2x3]
    'tensor to array:\n', tensor2array, # [[0 1 2], [3 4 5]]
)

矩阵点乘

data = [[1,2], [3,4]]
tensor = torch.FloatTensor(data)  # 转换成32位浮点 tensor

print(
    'matrix multiplication (matmul)\n',
    'numpy: ', np.matmul(data, data)\n,     # [[7, 10], [15, 22]]
    'torch: ', torch.mm(tensor, tensor)\n   # [[7, 10], [15, 22]]
)

变量`Variable`

在 Torch 中的 Variable 就是一个存放会变化的值的地理位置. 里面的值会不停的变化

Variable 计算时, 它会在后台搭建计算图（computational graph），将所有的计算步骤 (节点) 都连接起来, 最后进行误差反向传递的时候, 一次性将所有 variable 里面的修改幅度 (梯度) 都计算出来

import torch
from torch.autograd import Variable  # torch 中 Variable 模块

# 先定义 tensor
tensor = torch.FloatTensor([[1,2],[3,4]])

# 把 tensor 放到 Variable 里
variable = Variable(tensor, requires_grad=True)  #requires_grad表示是否参与误差反向传播, 是否要计算梯度

print(tensor)

1  2
3  4
[torch.FloatTensor of size 2x2]

print(variable)

Variable containing:
1  2
3  4
[torch.FloatTensor of size 2x2]

计算梯度

t_out = torch.mean(tensor*tensor)       # x^2
v_out = torch.mean(variable*variable)   # x^2
print(t_out)
print(v_out)    # 7.5

v_out.backward()    # 模拟 v_out 的误差反向传递

Variable 是计算图的一部分, 用来传递误差
v_out = 1/4 * sum(variable*variable) 这是计算图中的 v_out 计算步骤
针对于 v_out 的梯度就是, d(v_out)/d(variable) = 1/42variable = variable/2

print(variable.grad)    # 初始 Variable 的梯度

0.5000  1.0000
1.5000  2.0000

获取变量里的数据

直接print(variable)只会输出 Variable 形式的数据, 在很多时候是用不了的(比如想要用 plt 画图), 所以我们要转换一下, 将它变成 tensor 形式

print(variable)     #  Variable 形式

Variable containing:
1  2
3  4
[torch.FloatTensor of size 2x2]

print(variable.data)    # tensor 形式

1  2
3  4
[torch.FloatTensor of size 2x2]

print(variable.data.numpy())    # numpy 形式

[[ 1.  2.]
[ 3.  4.]]

常见激励函数

如果不用激励函数（其实相当于激励函数是f(x) = x），在这种情况下你每一层输出都是上层输入的线性函数，很容易验证，无论你神经网络有多少层，输出都是输入的线性组合，与没有隐藏层效果相当，这种情况就是最原始的感知机（Perceptron）了。

正因为上面的原因，才引入了非线性函数作为激励函数，这样深层神经网络就有意义了（不再是输入的线性组合，可以逼近任意函数）。

import torch
import torch.nn.functional as F     # 激励函数都在这
from torch.autograd import Variable

# 做一些假数据来观看图像
x = torch.linspace(-5, 5, 200)  # x data (tensor), shape=(100, 1)
x = Variable(x)
x_np = x.data.numpy()   # 换成 numpy array, 出图时用

# 常用的激励函数
y_relu = F.relu(x).data.numpy()
y_sigmoid = F.sigmoid(x).data.numpy()
y_tanh = F.tanh(x).data.numpy()
y_softplus = F.softplus(x).data.numpy()
# y_softmax = F.softmax(x)

# 画图
import matplotlib.pyplot as plt

plt.figure(1, figsize=(8, 6))
plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label='relu')
plt.ylim((-1, 5))
plt.legend(loc='best')

plt.subplot(222)
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid')
plt.ylim((-0.2, 1.2))
plt.legend(loc='best')

plt.subplot(223)
plt.plot(x_np, y_tanh, c='red', label='tanh')
plt.ylim((-1.2, 1.2))
plt.legend(loc='best')

plt.subplot(224)
plt.plot(x_np, y_softplus, c='red', label='softplus')
plt.ylim((-0.2, 6))
plt.legend(loc='best')

plt.show()

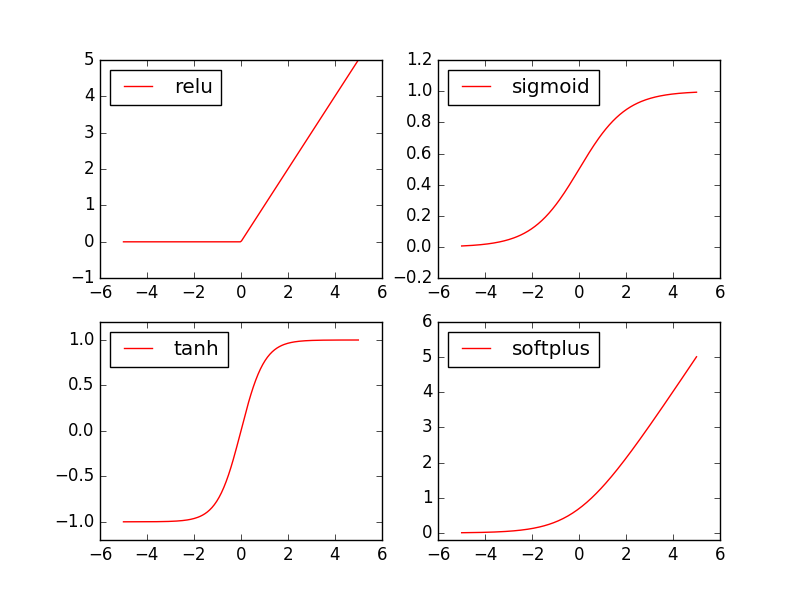
更全的激活函数公式跟图片点这个链接

示例1：回归任务

数据集

import torch
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())                 # noisy y data (tensor), shape=(100, 1)

# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

构建网络

先定义所有的层属性(init()), 然后再一层层搭建(forward(x))层于层的关系链接

import torch.nn.functional as F     # 激励函数

class Net(torch.nn.Module):                                  # 继承 torch 的 Module
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()                          # 继承 __init__ 功能
        # 定义每层用什么样的形式
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 隐藏层线性输出
        self.predict = torch.nn.Linear(n_hidden, n_output)   # 输出层线性输出

    def forward(self, x):   # 这同时也是 Module 中的 forward 功能
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.predict(x)             # 输出值
        return x

net = Net(n_feature=1, n_hidden=10, n_output=1)

print(net)  # net 的结构

Net (
(hidden): Linear (1 -> 10)
(predict): Linear (10 -> 1)
)

训练网络

# 这里用了最常用的随机梯度下降
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)  # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss()                         # 预测值和真实值的误差计算公式 (均方差)

for t in range(100):
    prediction = net(x)                 # 喂给 net 训练数据 x, 输出预测值

    loss = loss_func(prediction, y)     # 计算两者的误差

    optimizer.zero_grad()   # 清空上一步的残余更新参数值
    loss.backward()         # 误差反向传播, 计算参数更新值
    optimizer.step()        # 将参数更新值施加到 net 的 parameters 上

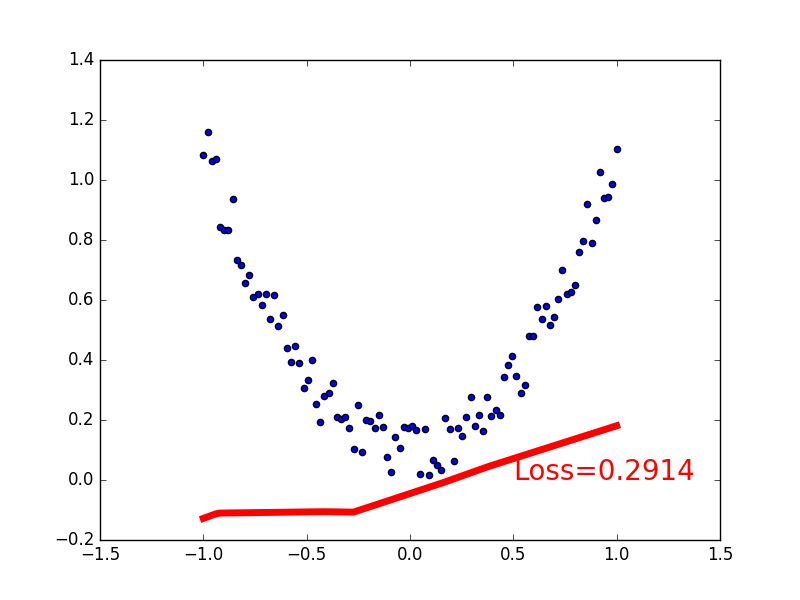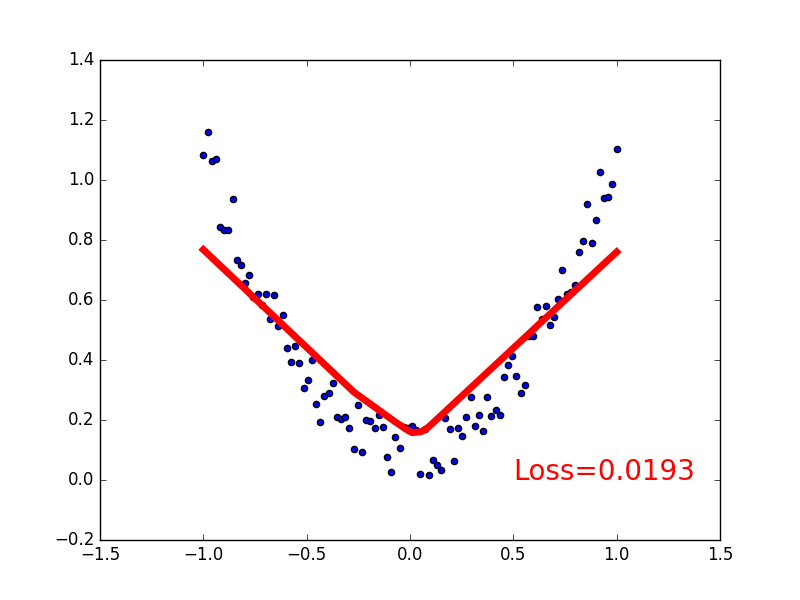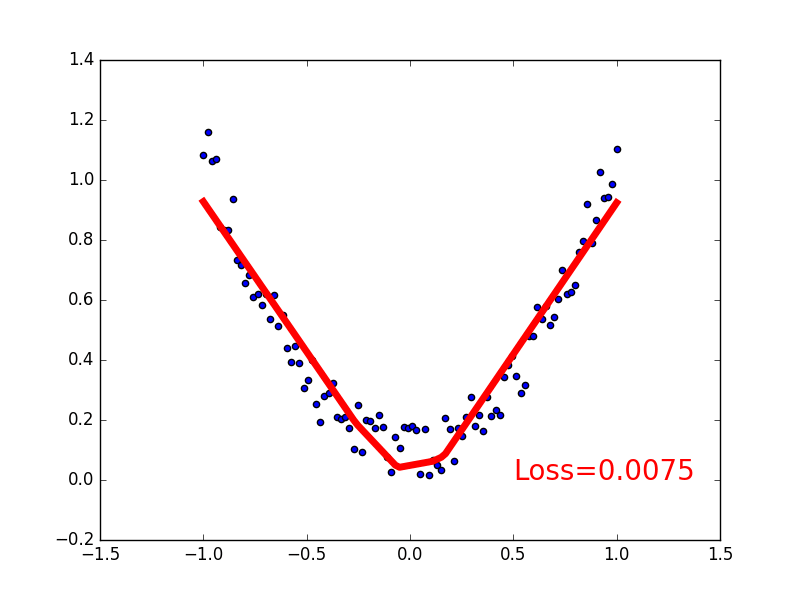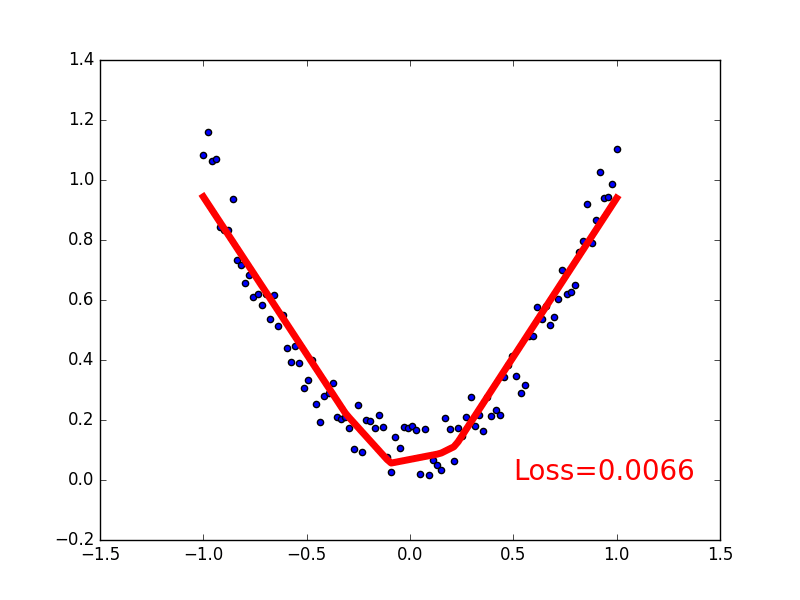
可视化

import matplotlib.pyplot as plt

plt.ion()   # 画图
plt.show()

for t in range(200):

    ...
    loss.backward()
    optimizer.step()

    # 接着上面来
    if t % 5 == 0:
        # plot and show learning process
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

示例2：分类任务

数据集

import torch
import matplotlib.pyplot as plt

# 假数据
n_data = torch.ones(100, 2)         # 数据的基本形态
x0 = torch.normal(2*n_data, 1)      # 类型0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100)               # 类型0 y data (tensor), shape=(100, 1)
x1 = torch.normal(-2*n_data, 1)     # 类型1 x data (tensor), shape=(100, 1)
y1 = torch.ones(100)                # 类型1 y data (tensor), shape=(100, 1)

# 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据)
x = torch.cat((x0, x1), 0).type(torch.FloatTensor)  # FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor)    # LongTensor = 64-bit integer

# plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
# plt.show()

# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

构建网络

import torch.nn.functional as F     # 激励函数

class Net(torch.nn.Module):                                  # 继承 torch 的 Module
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()                          # 继承 __init__ 功能
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 隐藏层线性输出
        self.out = torch.nn.Linear(n_hidden, n_output)       # 输出层线性输出

    def forward(self, x):
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.out(x)                 # 输出值, 但是这个不是预测值, 预测值还需要再另外计算
        return x

net = Net(n_feature=2, n_hidden=10, n_output=2) # 几个类别就几个 output

print(net)  # net 的结构

Net (
(hidden): Linear (2 -> 10)
(out): Linear (10 -> 2)
)

训练网络

optimizer = torch.optim.SGD(net.parameters(), lr=0.02)  # 传入 net 的所有参数, 学习率

# 算误差的时候, 注意真实值!不是! one-hot 形式的, 而是1D Tensor, (batch,)
# 但是预测值是2D tensor (batch, n_classes)
loss_func = torch.nn.CrossEntropyLoss()

for t in range(100):
    out = net(x)     # 喂给 net 训练数据 x, 输出分析值

    loss = loss_func(out, y)     # 计算两者的误差

    optimizer.zero_grad()   # 清空上一步的残余更新参数值
    loss.backward()         # 误差反向传播, 计算参数更新值
    optimizer.step()        # 将参数更新值施加到 net 的 parameters 上

可视化

import matplotlib.pyplot as plt

plt.ion()   # 画图
plt.show()

for t in range(100):

    ...
    loss.backward()
    optimizer.step()

    # 接着上面来
    if t % 2 == 0:
        plt.cla()
        # 过了一道 softmax 的激励函数后的最大概率才是预测值
        prediction = torch.max(F.softmax(out), 1)[1]
        pred_y = prediction.data.numpy().squeeze()
        target_y = y.data.numpy()
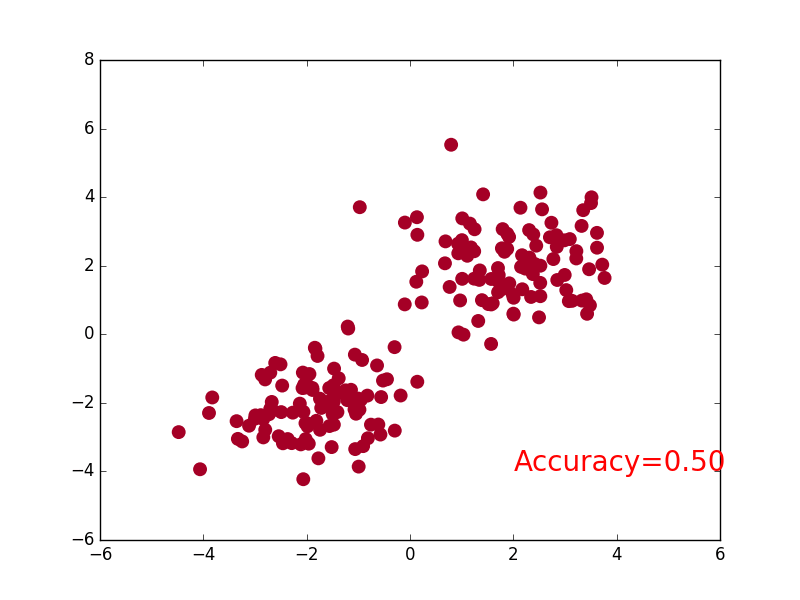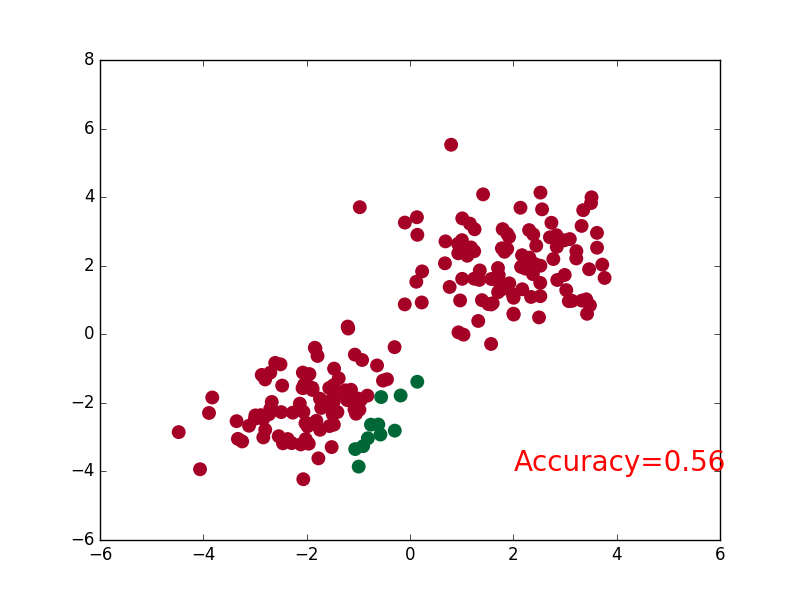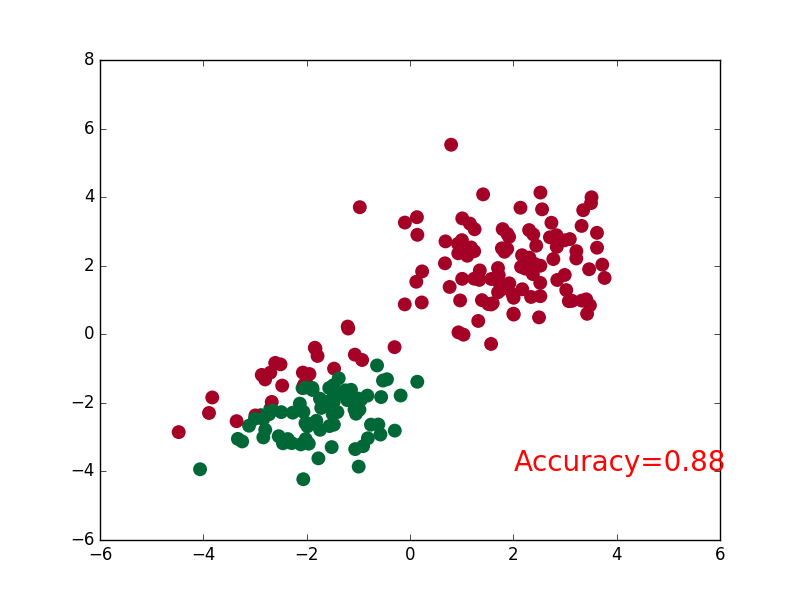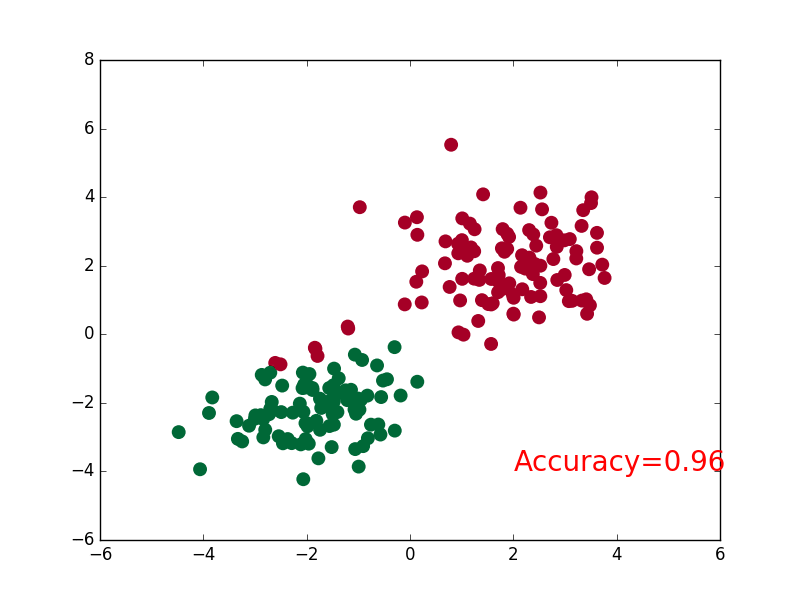
        plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
        accuracy = sum(pred_y == target_y)/200.  # 预测中有多少和真实值一样
        plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)

plt.ioff()  # 停止画图
plt.show()

For Deep Learning

numpy与tensor的转换

矩阵点乘

变量`Variable`

计算梯度

获取变量里的数据

常见激励函数

示例1：回归任务

数据集

构建网络

训练网络

可视化

示例2：分类任务

数据集

构建网络

训练网络

可视化

CATALOG

FEATURED TAGS

FRIENDS

numpy与tensor的转换

矩阵点乘

变量Variable

计算梯度

获取变量里的数据

常见激励函数

示例1：回归任务

数据集

构建网络

训练网络

可视化

示例2：分类任务

数据集

构建网络

训练网络

可视化

CATALOG

FEATURED TAGS

FRIENDS

变量`Variable`