Machine Learning Deep Learning

探索序列模型的本质

For Series Data

Posted by Jiayue Cai on November 4, 2018

Last updated on 2018-11-18…

序列数据如文本、语音、视频等，这类数据的样本间存在顺序关系，每个样本和它之前的样本存在关联。比如说，在文本中，一个词和它前面的词是有关联的；在气象数据中，一天的气温和前几天的气温是有关联的。

理论上 Simple RNN（或者叫 Vanilla RNN）就已经是图灵完备的了，能够模拟任何程序。但是实践中总是不尽如人意，因为存在性（存在一组模型设置能达到某个目的）和可学习性（真的通过训练能够找到这组参数设置）是两回事。

目前大约有三类机制解决长期依赖的学习问题，分别是门机制、跨尺度连接和特殊初始化（及其维持）。本文就门机制做了简述，其他请参考这个链接。另外，这篇文章可以加深理解。

一组观察数据定义为一个序列，从分布中可以观察出多个序列。

早期

最简模型

一个序列 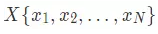的最简单模型为

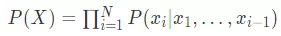
也就是说，序列里的每一个元素都和排在它前面的所有元素直接相关。当然，这个模型存在致命的问题：它的复杂度会爆炸性增长，O(N!)。

HMM

隐马尔科夫模型（HMM）定义每个元素只和离它最近的k个元素相关，解决了复杂度暴增的问题，模型为

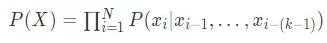
当k=1时，模型变为

只考虑观察值X的模型有时表现力不足，因此需要加入隐变量，将观察值建模成由隐变量所生成。

隐变量的好处在于，它的数量可以比观察值多，取值范围可以比观察值更广，能够更好的表达有限的观察值背后的复杂分布。加入了隐变量h的马尔科夫模型称为隐马尔科夫模型。

隐马尔科夫模型实际上建模的是观察值X，隐变量h和模型参数θ的联合分布，HMM的模型长度T是事先固定的，模型参数不共享，其复杂度为O(T)。

RNN(0门控)

RNN

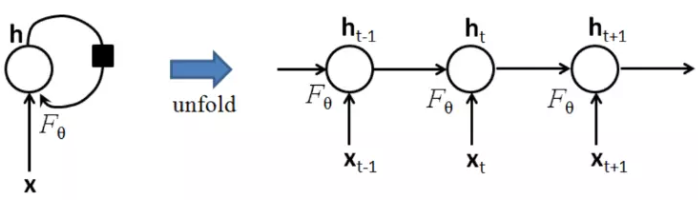把序列视作时间序列，隐含层hh的自连接边实际上是和上一时刻的h相连（上面左图）。在每一个时刻t，ht的取值是当前时刻的输入xt，和上一时刻的隐含层值ht-1的一个函数：

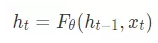
将h层的自连接展开，就成为了上图右边的样子，看上去和HMM很像。两者最大的区别在于，RNN的参数是跨时刻共享的。也就是说，对任意时刻t，ht-1到ht，以及xt到ht的网络参数都是相同的。

共享参数的思想和和卷积神经网络（CNN）是相通的，CNN在二维数据的空间位置之间共享卷积核参数，而RNN则是在序列数据的时刻之间共享参数。共享参数使得模型的复杂度大大减少，并使RNN可以适应任意长度的序列，带来了更好的可推广性。

classRNN:
    def step(self, x):

        # update the hidden state

        self.h = np.tanh(np.dot(self.W_hh, self.h) + np.dot(self.W_xh, x))

        # compute the output vector

        y = np.dot(self.W_hy, self.h)

    return y

RNN变种

1、双向RNN

单向RNN的问题在于t时刻进行分类的时候只能利用t时刻之前的信息， 但是在t时刻进行分类的时候可能也需要利用未来时刻的信息。双向RNN（bi-directional RNN）模型正是为了解决这个问题， 双向RNN在任意时刻 t 都保持两个隐藏层，一个隐藏层用于从左往右的信息传播记作， 另一个隐藏层用于从右往左的信息传播记作。

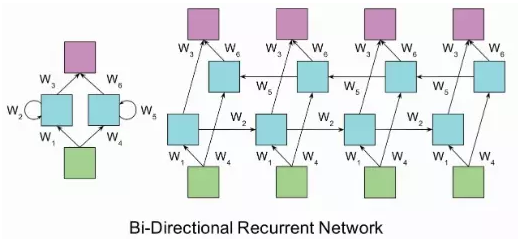
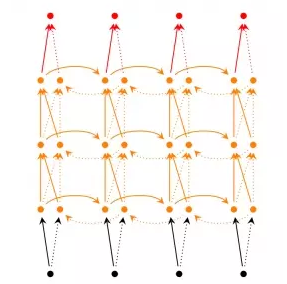
2、Deep RNN

Deep(Bidirectional)RNNs与Bidirectional RNNs相似，只是对于每一步的输入有多层网络。这样，该网络便有更强大的表达与学习能力，但是复杂性也提高了，同时需要更多的训练数据。

梯度消失和梯度爆炸

RNN训练困难的主要原因在于隐藏层参数w的传播：由于误差传播在展开后的RNN上，无论在前向传播过程还是在反向传播过程中w都会乘上多次，导致了梯度消失和梯度爆炸问题。

梯度爆炸和梯度消失问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。

梯度消失 Gradient Vanishing

如果梯度很小的话（<1），乘上多次指数级下降，对输出几乎就没有影响了

对于梯度消失问题有很多不同的方案：

  • 有效初始化+ReLU激活函数能够得到较好效果
  • 算法上的优化，例如截断的BPTT算法
  • 模型上的改进，例如LSTM、GRU单元都可以有效解决长期依赖问题
  • 在BPTT算法中加入skip connection，此时误差可以间歇的向前传播
  • 加入一些Leaky Units，思路类似于skip connection

梯度爆炸 Gradient Exploding

反过来，如果梯度很大的话，乘上多次指数级增加，又导致了梯度爆炸

  • 模型在训练过程中，权重变化非常大
  • 模型在训练过程中，权重变成NaN值
  • 每层的每个节点在训练时，其误差梯度值一直是大于1.0

当然了，这个问题其实存在于任何深度神经网络中，只是由于RNN的递归结构导致其尤其明显。对于梯度爆炸问题，可以通过截断的方式来有效避免：

门机制模型

LSTM(3门控)

LSTM 全称叫 Long Short-Term Memory networks，它和传统 RNN 唯一的不同就在与其中的神经元（感知机）的构造不同。传统的 RNN 每个神经元和一般神经网络的感知机没啥区别，但在 LSTM 中，每个神经元是一个“记忆细胞”（元胞状态，Cell State），将以前的信息连接到当前的任务中来。每个LSTM细胞里面都包含三个门

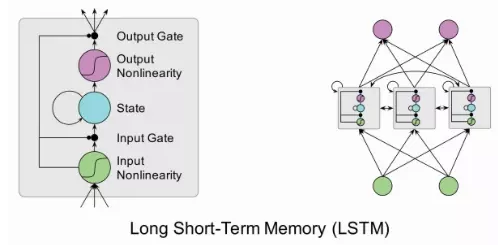
遗忘门（forget gate): 控制前一步记忆状态中的信息有多大程度被遗忘：一个Sigmoid层决定我们要更新哪些信息，并由一个tanh层创造了一个新的候选值（结果在(-1, 1)(−1,1)范围）

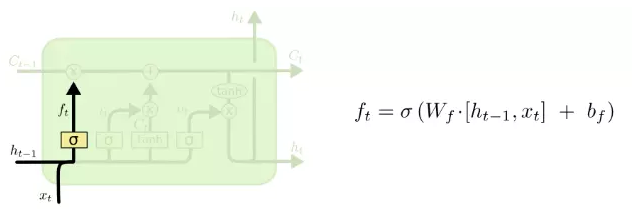
输入门（input gate）: 控制当前计算的新状态以多大的程度更新到记忆状态中：一个Sigmoid层，观察ht-1和xt，对于元胞状态ct-1中的每一个元素，输出一个0~1之间的数。1表示“完全保留该信息”，0表示“完全丢弃该信息”：

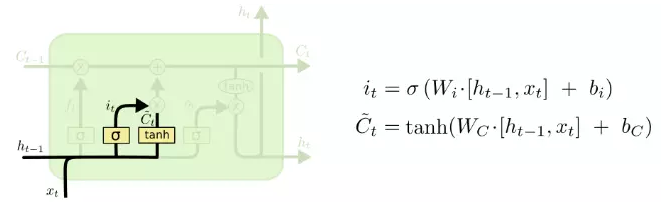
记忆状态 C间的状态转移由输入门和遗忘门共同决定：

输出门（output gate）：控制当前的输出有多大程度取决于当前的记忆状态，即控制哪些信息需要输出：

典型的工作流为：在“输入门”中，根据当前的数据流来控制接受细胞记忆的影响；接着，在 “遗忘门”里，更新这个细胞的记忆和数据流；然后在“输出门”里产生输出更新后的记忆和数据流。

LSTM 模型的关键之一就在于这个“遗忘门”， 它能够控制训练时候梯度在这里的收敛性（从而避免了 RNN 中的梯度 vanishing/exploding 问题），同时也能够保持长期的记忆性。

如果我们把LSTM的input gate全部 置1，forget gate全部置0（总是忘记之前的信息），output gate全部置1（把cell state中的信息全部输出），这样LSTM就变成一个标准的RNN。

目前 LSTM 模型在实践中取得了非常好的效果， 只需要训练一个两三层的LSTM, 它就可以：模仿保罗·格雷厄姆进行写作、生成维基百科的 markdown 页面、手写识别、写代码

GRU(2门控)

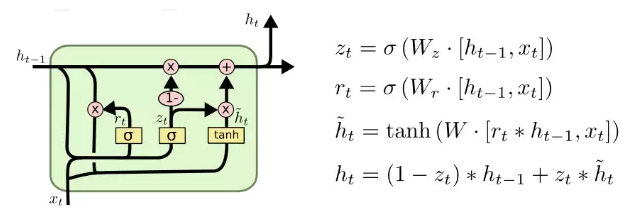
GRU 相比 LSTM 的改动：

  • GRU 把遗忘门和输入门合并为更新门（Update Gate） z，并使用重置门（reset） r 代替输出门
  • 合并了记忆状态 C 和隐藏状态 h

更新门 z用于控制前一时刻的状态信息被融合到当前状态中的程度：

重置门 r用于控制忽略前一时刻的状态信息的程度：

LSTM（左）与GRU（右）对比：

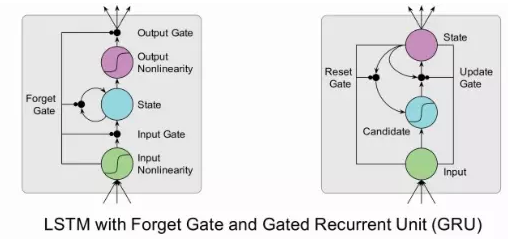
GRU更新过程：

MGU(1门控)

信息闸门的原理另一个巧妙的理解是某种“惯性” 机制，隐变量的状态更新不是马上达到指定的值，而是缓慢达到这个值， 如同让过去的信息多了一层缓冲，而要多少缓冲则是由一个叫做遗忘门的东西决定的。 如此我们发现其实这几个新增加的东西最核心的就是信息的闸门遗忘门。

根据这一原理，我们可以抓住本质简化lstm，如GRU或极小GRU。 其实我们只需要理解这个模型就够了，而且它们甚至比lstm更快更好。

第一个方程f即遗忘门， 第二方程如果你对比先前的RNN会发现它是一样的结构， 只是让遗忘门f来控制每个神经元放多少之前信息出去（改变其它神经元的状态）， 第三个方程描述“惯性” ，即最终每个神经元保持多少之前的值，更新多少。

谷歌翻译流程

首先，翻译是沟通两个不同的语言， 而你要这个沟通的本质是因为它们所表达的事物是相同的， 我们自己的大脑做翻译的时候，也是根据它们所表达的概念相同比如苹果-vs-apple来沟通两个语言的。如果汉语是输入，英语是输出，神经网络事实上做的是这样一件事：

  • Encoding： 用一个LSTM把汉语变成神经代码
  • Decoding：用另一个LSTM把神经代码转化为英文

第一个lstm的输出是第二个lstm的输入，两个网络用大量语料训练好即可。 Google 2016 加入了attention机制 ，使得google的翻译系统就更接近人脑。

Attention and Augmented Recurrent Neural Networks见我的上一篇博客。

用FSA解释RNN

From 周志华团队。机器之心链接、论文链接。

在这篇论文中，周志华等研究者尝试从 RNN 学习 FSA，他们首先验证了除不带门控的经典 RNN 外，其它门控 RNN 变体的隐藏状态同样也具有天然的集群属性。

然后他们提出了两种方法，其一是高效的聚类方法 k-means++。另外一种方法根据若相同序列中隐藏状态相近，在几何空间内也相近的现象而提出，这一方法被命名为 k-means-x。

随后研究者通过设计五个必要的元素来学习 FSA，即字母表、一组状态、初始状态、一组接受状态和状态转换，他们最后将这些方法应用到了模拟数据和真实数据中。

对于人工模拟数据，研究者首先表示我们可以理解在运行过程学习到的 FSA。然后他们展示了准确率和集群数量之间的关系，并表示门控机制对于门控 RNN 是必要的，并且门越少越好。这在一定程度上解释了为什么只有一个门控的 MGU 在某种程度上优于其它门控 RNN。

对于情感分析这一真实数据，研究者发现在数值计算的背后，RNN 的隐藏状态确实具有区分语义差异性的能力。因为在对应的 FSA 中，导致正类/负类输出的词确实在做一些正面或负面的人类情感理解。

CATALOG
    FEATURED TAGS
    Develop C++ Python Simulation Machine Learning Feature Engineering Recommending System Tensorflow Deep Learning NLP Big Data Image Reinforcement Learning Computational Advertising Business
    FRIENDS