Last updated on 2019-10-30…
强化学习本质就是动态规划,Graph Embedding本质就是图论(dfs的DeepWalk,bfs的GCN),掌握本质才能迸发出大的创新。
趁着秋招刚结束的余热,写这篇博客一方面为了复习跟备忘,另一方面为了督促自己学习。(弥补自己大一当时没坚持下来的遗憾…)
数学结构
Hash表
【POJ 3349】Snowflake Snow Snowflakes
题 意:判断所有的雪花中是否有相似的。相似的判断依据就是其中某一雪花从任意一位置顺时针或逆时针按顺序组成6位数中的所有可能是否有与另一个雪花完全相同的,若有,则说明这两个雪花相似,否则不相似。而题目就是要据此条件判断所有的雪花中是否存在相似的雪花。
分 析:朴素的算法就是枚举,对任意两个雪花都进行这样的判断。这样的时间复杂度接近为O(n^2),而题目中n的最大值为100000,显然会超时,这里采用哈希查找的办法解决,并采用链地址法解决冲突。
思 路:若判断在该哈希位置已经存在雪花,那么不管是冲突的,还是本身key值相等的,统一用上面的方法对该哈希位置上的每一个雪花进行相似比较。若存在与其相似的雪花,则直接返回,主函数就不需要在对后续输入的雪花进行相似判断了,否则就将该雪花利用头插法(或尾插法)插入到该哈希位置的链表中。
#include <bits/stdc++.h>
using namespace std;
#define N 100001
typedef struct node{
int data[6];
struct node* last;
}point;
int n, dp[6];
point snow[N];
void init(){
for(int i=0;i<N;i++) snow[i].last=NULL;
}
bool issame(int* white){
for(int i=0;i<6;i++){ //这里为了解决同构的问题,我们必须要考虑顺时针和逆时针,在这里我们引入了如下的方法进行优化,值得学习
if((dp[0]==white[i] && dp[1]==white[(i+1)%6] && dp[2]==white[(i+2)%6] &&
dp[3]==white[(i+3)%6] && dp[4]==white[(i+4)%6] && dp[5]==white[(i+5)%6]) ||
(dp[0]==white[i] && dp[1]==white[(i+5)%6] && dp[2]==white[(i+4)%6] &&
dp[3]==white[(i+3)%6] && dp[4]==white[(i+2)%6] && dp[5]==white[(i+1)%6]))
return true;
}
return false;
}
bool find(int key){
point* k=snow[key].last;
while(k!=NULL){
if(issame(k->data)) return true;
k=k->last;
}
return false;
}
void insert(int key){
point* k=new point;
for(int i=0;i<6;i++) k->data[i]=dp[i];
k->last=snow[key].last;
snow[key].last=k;
}
int main(){
bool ok=false;
init();
scanf("%d",&n);
for(int i=1;i<=n;i++){
int sum=0;
for(int j=0;j<6;j++) scanf("%d",&dp[j]),sum+=dp[j];
sum=sum%N;
if(find(sum)) ok=true;
else insert(sum);
}
if(ok) printf("Twin snowflakes found.\n");
else printf("No two snowflakes are alike.\n");
return 0;
}
线性结构
例如数组、栈、队列、双端队列等,略
集合结构
幷查集
并查集是若干个不相交集合,能够实现较快的合并和判断元素所在集合的操作。(eg.求无向图的连通分量个数、Kruskar算法求最小生成树)
并查集的操作:
1、Make_Set(x) 把每一个元素初始化为一个集合
- 初始化后每一个元素的父亲节点是它本身,每一个元素的祖先节点也是它本身(也可以根据情况而变)。
2、Find_Set(x) 查找一个元素所在的集合
- 查找一个元素所在的集合,其精髓是找到这个元素所在集合的祖先!这个才是并查集判断和合并的最终依据。
- 判断两个元素是否属于同一集合,只要看他们所在集合的祖先是否相同即可。
- 合并两个集合,也是使一个集合的祖先成为另一个集合的祖先。
3、Union(x,y) 合并x,y所在的两个集合
- 利用Find_Set找到其中两个集合的祖先,将一个集合的祖先指向另一个集合的祖先。
并查集的优化:
1、Find_Set(x)时 路径压缩
- 寻找祖先时我们一般采用递归查找,但是当元素很多亦或是整棵树变为一条链时,每次Find_Set(x)都是O(n)的复杂度,有没有办法减小这个复杂度呢?
- 答案是肯定的,这就是路径压缩,即当我们经过
递推找到祖先节点后,回溯的时候顺便将它的子孙节点都直接指向祖先,这样以后再次Find_Set(x)时复杂度就变成O(1)了;可见,路径压缩方便了以后的查找。
2、Union(x,y)时 按秩合并
- 即合并的时候将元素少的集合合并到元素多的集合中,这样合并之后树的高度会相对较小。
int father[MAX]; /* father[x]表示x的父节点*/
int rank[MAX]; /* rank[x]表示x的秩*/
/* 初始化集合*/
void Make_Set(int x){
father[x] = x; //根据实际情况指定的父节点可变化
rank[x] = 0; //根据实际情况初始化秩也有所变化
}
/* 查找x元素所在的集合,回溯时压缩路径*/
int Find_Set(int x){
if (x != father[x])
father[x] = Find_Set(father[x]); //这个回溯时的压缩路径是精华
return father[x];
}
/* 按秩合并x,y所在的集合。下面的那个if else结构不是绝对的,具体根据情况变化。但是,宗旨是不变的即,按秩合并,实时更新秩。*/
void Union(int x, int y){
x = Find_Set(x);
y = Find_Set(y);
if (x == y) return;
if (rank[x] > rank[y])
father[y] = x;
else{
if (rank[x] == rank[y])
rank[y]++;
father[x] = y;
}
}
思 路:把确定了相对关系的节点放在同一棵树中,每个节点对应的 r[]值记录他与根节点的关系:
- 0:同类
- 1:被父亲节点吃
- 2: 吃父亲节点
#include <bits/stdc++.h>
using namespace std;
const int maxn = 50000+10;
int p[maxn]; //存父节点
int r[maxn];//存与父节点的关系 0 同一类,1被父节点吃,2吃父节点
void set(int n) //初始化{
for(int x = 1; x <= n; x++){
p[x] = x; //开始自己是自己的父亲节点
r[x] = 0;//开始自己就是自己的父亲,每一个点均独立
}
}
int find(int x) //找父亲节点{
if(x == p[x]) return x;
int t = p[x];
p[x] = find(p[x]);
r[x] = (r[x]+r[t])%3; //回溯由子节点与父节点的关系和父节点与根节点的关系找子节点与根节点的关系
return p[x];
}
void Union(int x, int y, int d){
int fx = find(x);
int fy = find(y);
p[fy] = fx; //合并树 注意:被 x 吃,所以以 x 的根为父
r[fy] = (r[x]-r[y]+3+(d-1))%3; //对应更新与父节点的关系
}
int main(){
int n, m;
scanf("%d%d", &n, &m);
set(n);
int ans = 0;
int d, x, y;
while(m--){
scanf("%d%d%d", &d, &x, &y);
if(x > n || y > n || (d == 2 && x == y)) ans++; //如果节点编号大于最大编号,或者自己吃自己,说谎
else if(find(x) == find(y)){ //如果原来有关系,也就是在同一棵树中,那么直接判断是否说谎
if(d == 1 && r[x] != r[y]) ans++; //如果 x 和 y 不属于同一类
if(d == 2 && (r[x]+1)%3 != r[y]) ans++; // 如果 x 没有吃 y (注意要对应Uinon(x, y)的情况,否则一路WA到死啊!!!)
}
else Union(x, y, d); //如果开始没有关系,则建立关系
}
printf("%d\n", ans);
return 0;
}
其他:【POJ 1308】Is It A Tree?、【POJ 1611】The Suspects、【POJ 1986】Distance Queries、【POJ 1988】Cube Stacking
莫队算法
题 意:有n个女生,每个女生都属于一个教室,现在要访问这些女生,就要进入教室,每次进入一个教室只能访问该教室的一个女生。 现在要问对于[L,R]之间的女生全部访问,一共有多少种不同的访问教室的方式?
思 路:因为最后的方案按照教室的不同来划分,那就与教室内部的女生访问顺序没有关系,那么只要拿所有女生的访问的排列数除以每个教室女生的排列数即可。 区间查询问题,不涉及修改操作,而且区间改变一个单位的大小只需要O(1)的时间,典型的莫队算法可以处理的类型。 分块加速,以及要求逆元。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD = 1e9 + 7;
const int MAXN = 3e4 + 10;
LL inv[MAXN];
void init() {
inv[0] = inv[1] = 1;
for (int i = 2; i <= 30000; i++)
inv[i] = (MOD - MOD / i) * inv[MOD % i] % MOD;
}
LL cur, num;
int cnt[MAXN], a[MAXN], p[MAXN];
void add(int pos) {
++num; ++cnt[a[pos]];
cur = cur * num % MOD;
cur = cur * inv[cnt[a[pos]]] % MOD;
}
void del(int pos) {
cur = cur * inv[num] % MOD;
cur = cur * cnt[a[pos]] % MOD;
cnt[a[pos]]--; num--;
}
struct Query {
int l, r, id;
bool operator < (const Query &rhs) const {
return p[l] == p[rhs.l] ? r < rhs.r : p[l] < p[rhs.l];
}
} q[MAXN];
LL ans[MAXN];
int main() {
//freopen("in.txt", "r", stdin);
init();
int T;
scanf("%d", &T);
while (T--) {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
scanf("%d", &a[i]);
int block = ceil(sqrt(n));
for (int i = 1; i <= n; i++) p[i] = (i - 1) / block;
for (int i = 1; i <= m; i++) {
scanf("%d%d", &q[i].l, &q[i].r);
q[i].id = i;
}
sort(q + 1, q + 1 + m);
memset(cnt, 0, sizeof(cnt));
cur = 0, num = 0;
add(1);
cur = 1;
int l = 1, r = 1;
for (int i = 1; i <= m; i++) {
while (r > q[i].r) {
del(r);
r--;
}
while (r < q[i].r) {
++r;
add(r);
}
while (l > q[i].l) {
--l;
add(l);
}
while (l < q[i].l) {
del(l);
l++;
}
ans[q[i].id] = cur;
}
for (int i = 1; i <= m; i++)
printf("%I64d\n", ans[i]);
}
return 0;
}
统计结构
树状数组
题 意:提供一个M×N的矩阵,其中每一个格子中的数不是1就是0,开始时每个格子的值为0。
- 修改操作(C):取反矩阵中的数字,给出矩阵的左上角坐标(x1,y1)和右下角的坐标(x2,y2)。
- 查询操作(Q):查询第x行第y列的格子中的数子是什么。
分 析:根据这个题目中介绍的这个矩阵中的数的特点不是1就是0,这样我们只需记录每个格子改变过几次,即可判断这个格子的数字。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1010;
int treeNum[MAXN][MAXN];
int lowbit(int x){
return x&(-x);
}
long long getSum(int x , int y){
long long sum = 0;
for(int i = x ; i > 0 ; i -= lowbit(i))
for(int j = y ; j > 0 ; j -= lowbit(j))
sum += treeNum[i][j];
return sum;
}
void add(int x , int y , int val){
for(int i = x ; i < MAXN ; i += lowbit(i))
for(int j = y ; j < MAXN ; j += lowbit(j))
treeNum[i][j] += val;
}
void solve(int m){
char ch;
int x , y;
int x1 , y1 , x2 , y2;
memset(treeNum , 0 , sizeof(treeNum));
while(m--){
scanf("%c" , &ch);
if(ch == 'C'){
scanf("%d%d" , &x1 , &y1);
scanf("%d%d%*c" , &x2 , &y2);
// update
add(x1 , y1 , 1);
add(x2+1 , y1 , -1);
add(x1 , y2+1 , -1);
add(x2+1 , y2+1 , 1);
}
else{
scanf("%d%d%*c" , &x , &y);
int ans = getSum(x , y);
printf("%d\n" , ans%2);
}
}
}
int main(){
int cas;
int n , m;
bool isFirst = true;
scanf("%d" , &cas);
while(cas){
scanf("%d%d%*c" , &n , &m);
solve(m);
if(--cas)
puts("");
}
return 0;
}
线段树
关于线段树节点维护的信息(以线保留型线段树为例):
- cnt:保存的是当前节点被覆盖的值。(cnt信息不上传也不下传,属于线保留型。)
- sum:表示该节点控制的区域内,被覆盖的最大值。(由于初始cnt和sum都为0,所以可以用memset代替build)
- PushUp操作和update操作是必须的.
【POJ 2482】Stars in Your Window
题 意:有很多点在二维平面内,每个点有一个价值,给你一个平行坐标轴的矩形,只可以移动矩形,问矩形最多能包括多少价值和的点.
分 析:本题首先要转换一下,我们用矩形的中心点来描述这个矩形,然后对于每个星星,我们建立一个矩形中心的活动范围,即矩形中心在该范围内活动就可以覆盖到该星星。
思 路:其实这个新矩形与原来的矩形长和宽都是相同的,所以我们要求的问题就变成了:
- 任意一个区域(肯定也是矩形的)最多能被矩形覆盖的最大值。即假如有价值为5和价值为3的矩形覆盖了一个区域,但是不仅仅是边界相交,那么这片区域的价值为8。
#include <bits/stdc++.h>
using namespace std;
#define lson i*2,l,m
#define rson i*2+1,m+1,r
const int MAXN=20000+5; //必须为2W,因为点有1W个,所以扫描线2W个,不同的Y坐标最多有2W个
int cnt[MAXN*4],sum[MAXN*4];
double Y[MAXN];
struct seg{
double l,r,h;
int d;
seg(){}
seg(double a,double b,double c,int d):l(a),r(b),h(c),d(d){}
bool operator <(const seg&b)const{
if(h == b.h) return d<b.d;
return h<b.h;
}
}ss[MAXN];
void PushUp(int i){
sum[i]=max(sum[i*2],sum[i*2+1]) + cnt[i];
}
void update(int ql,int qr,int v,int i,int l,int r){
if(ql<=l && r<=qr){
cnt[i]+=v;
sum[i]+=v;
return ;
}
int m=(l+r)>>1;
if(ql<=m) update(ql,qr,v,lson);
if(m<qr) update(ql,qr,v,rson);
PushUp(i);
}
int main(){
int n;
double w,h;
while(scanf("%d%lf%lf",&n,&w,&h)==3){
if(n==0){
printf("0\n");
continue;
}
double x,y;
int val;
int cnt_y=0,cnt_ss=0;//记录有多少个Y值和扫描线
for(int i=1;i<=n;i++){
scanf("%lf%lf%d",&x,&y,&val);
ss[cnt_ss++] = seg(y-h/2,y+h/2,x-w/2,val);
ss[cnt_ss++] = seg(y-h/2,y+h/2,x+w/2,-val);
Y[cnt_y++] = y-h/2;
Y[cnt_y++] = y+h/2;
}
sort(ss,ss+cnt_ss);
sort(Y,Y+cnt_y);
cnt_y = unique(Y,Y+cnt_y)-Y;
int ans=0;
memset(cnt,0,sizeof(cnt));
memset(sum,0,sizeof(sum));
for(int i=0;i<cnt_ss-1;i++){
int ql=lower_bound(Y,Y+cnt_y,ss[i].l)-Y;
int qr=lower_bound(Y,Y+cnt_y,ss[i].r)-Y-1;
if(ql<=qr) update(ql,qr,ss[i].d,1,0,cnt_y-1);
ans=max(ans,sum[1]);
}
printf("%d\n",ans);
}
}
题 意:求n个矩形面积的并(1 <= n <= 100,坐标范围:0 <= x1 < x2 <= 100000;0 <= y1 < y2 <= 100000)。
思 路:提取出所有矩形的所有纵向边作为扫描线,从左往右扫描。
- 每处理一条扫描线时,下一条扫描线与当前扫描线的距离乘上当前已覆盖纵向边的长度是一个部分面积,将这些面积累加起来就是n个矩形面积的并。
- 当前覆盖到纵向边长度可通过线段树来维护。
空间上要求先对所有点的纵坐标进行离散化,总时间复杂度为O(nlogn)。
#include <bits/stdc++.h>
using namespace std;
#define lc (o<<1)
#define rc ((o<<1)+1)
const int MAXN = 100 + 10;
double y[MAXN<<1];
int cnt;
struct Scanline {
double x;
double y1, y2;
bool is_left;
bool operator < (const Scanline& e) const {
return x < e.x;
}
} scanlines[MAXN<<1];
struct Node {
int L, R;
double len;
int cover;
} nodes[MAXN<<3];
int point_to(double x) {
return lower_bound(y, y + cnt, x) - y;
}
void build(int o, int L, int R) {
nodes[o].L = L;
nodes[o].R = R;
nodes[o].len = 0;
nodes[o].cover = 0;
if(L + 1 == R) return;
int M = (L + R) >> 1;
build(lc, L, M);
build(rc, M, R);
}
void maintain_len(int o) {
if(nodes[o].cover > 0)
nodes[o].len = y[nodes[o].R] - y[nodes[o].L];
else if(nodes[o].L + 1 == nodes[o].R)
nodes[o].len = 0;
else
nodes[o].len = nodes[lc].len + nodes[rc].len;
}
void my_insert(int o, int ql, int qr) {
if(ql <= nodes[o].L && nodes[o].R <= qr) {
nodes[o].cover++;
maintain_len(o);
return;
}
int M = (nodes[o].L + nodes[o].R) >> 1;
if(ql < M) my_insert(lc, ql, qr);
if(qr > M) my_insert(rc, ql, qr);
maintain_len(o);
}
void my_delete(int o, int ql, int qr) {
if(ql <= nodes[o].L && nodes[o].R <= qr) {
nodes[o].cover--;
maintain_len(o);
return;
}
int M = (nodes[o].L + nodes[o].R) >> 1;
if(ql < M) my_delete(lc, ql, qr);
if(qr > M) my_delete(rc, ql, qr);
maintain_len(o);
}
int main(){
int n, kase = 0;
double x1, y1, x2, y2;
while(scanf("%d", &n) == 1 && n) {
for(int i = 0; i < n; i++) {
scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
scanlines[i<<1].x = x1;
scanlines[i<<1].y1 = y1;
scanlines[i<<1].y2 = y2;
scanlines[i<<1].is_left = true;
scanlines[(i<<1)+1].x = x2;
scanlines[(i<<1)+1].y1 = y1;
scanlines[(i<<1)+1].y2 = y2;
scanlines[(i<<1)+1].is_left = false;
y[i<<1] = y1;
y[(i<<1)+1] = y2;
}
sort(y, y + 2*n);
cnt = unique(y, y + 2*n) - y;
sort(scanlines, scanlines + 2*n);
build(1, 0, cnt-1);
double area = 0;
for(int i = 0; i < 2*n-1; i++) {
if(scanlines[i].is_left)
my_insert(1, point_to(scanlines[i].y1), point_to(scanlines[i].y2));
else
my_delete(1, point_to(scanlines[i].y1), point_to(scanlines[i].y2));
area += (scanlines[i+1].x - scanlines[i].x) * nodes[1].len;
}
printf("Test case #%d\n", ++kase);
printf("Total explored area: %.2f\n\n", area);
}
return 0;
}
字符结构
前缀树
题 意:给你许多字符串,然后让你找出最短的前缀字符串。但不能跟下面的单词的前缀相同。 思 路:trie建树,设置一个变量num,计算每个单词出现的次数。查找的时候如果num = 1则说明这是第一次出现过的单词,直接返回。
#include <bits/stdc++.h>
using namespace std;
struct Trie{
int num,next[30];
}trie[1005*30];
int e;
char str[1005][30],output[30];
void Insert (char str[]){
int i,p=1;
for (i=0;str[i];i++){
if (trie[p].next[str[i]-'a']==0){ //构造新的节点
trie[p].next[str[i]-'a']=++e;
trie[e].num=0;
}
p=trie[p].next[str[i]-'a'];
trie[p].num++;
}
}
void Search (char str[]){
int i,p=1;
for (i=0;str[i];i++){
if (trie[p].num==1)
return;
printf("%c",str[i]);
p=trie[p].next[str[i]-'a'];
}
}
int main (){
int n=0;
e=1;
while (~scanf("%s",str[n]))
Insert(str[n++]);
for (int i=0;i<n;i++){
printf("%s ",str[i]);
Search (str[i]);
printf("\n");
}
return 0;
}
后缀树
题 意:求两个串的最长公共子串长度,即输入两个长度不超过100000的字符串,输出这两个串的最长公共子串长度。
分 析:如果考虑使用动态规划来求解,100000×100000的复杂度显然是远远不能满足我们的需求的。
思 路:后缀数组,将两个串连在一起后求height[i]数组(连一起时中间要加一个隔离字符避免匹配越界),对于每个i,如果sa[i-1] < len且sa[i] > len(len为第一个串的串长),说明这两个相邻的后缀分别属于两个串,那么就用这个height[i]去更新答案,之所以可以这样做是因为做完后缀数组后所有后缀是按字典序排的,那么任意两个后缀的最长公共前缀长度不会超过字典序在这两个后缀之间的两个相邻后缀的height值。
#include <bits/stdc++.h>
using namespace std;
#define maxn 200002
int t1[maxn],t2[maxn],c[maxn],r[maxn],sa[maxn],rank[maxn],height[maxn];
bool cmp(int *r,int a,int b,int l){
return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(int str[],int sa[],int rank[],int height[],int n,int m){
n++;
int i,j,p,*x=t1,*y=t2;
for(i=0;i<m;i++)c[i]=0;
for(i=0;i<n;i++)c[x[i]=str[i]]++;
for(i=1;i<m;i++)c[i]+=c[i-1];
for(i=n-1;i>=0;i--)sa[--c[x[i]]]=i;
for(j=1;j<=n;j<<=1){
p=0;
for(i=n-j;i<n;i++)y[p++]=i;
for(i=0;i<n;i++)if(sa[i]>=j)y[p++]=sa[i]-j;
for(i=0;i<m;i++)c[i]=0;
for(i=0;i<n;i++)c[x[y[i]]]++;
for(i=1;i<m;i++)c[i]+=c[i-1];
for(i=n-1;i>=0;i--)sa[--c[x[y[i]]]]=y[i];
swap(x,y);
p=1;x[sa[0]]=0;
for(i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
if(p>=n)break;
m=p;
}
int k=0;
n--;
for(i=0;i<=n;i++)rank[sa[i]]=i;
for(i=0;i<n;i++)
{
if(k)k--;
j=sa[rank[i]-1];
while(str[i+k]==str[j+k])k++;
height[rank[i]]=k;
}
}
char a[maxn],b[maxn];
int main(){
while(~scanf("%s%s",a,b)){
int la=strlen(a),lb=strlen(b);
for(int i=0;i<la;i++)r[i]=a[i];
r[la]='#';
for(int i=0;i<lb;i++)r[i+la+1]=b[i];
r[la+lb+1]=0;
int n=la+lb+1;
da(r,sa,rank,height,n,128);
int ans=0;
for(int i=2;i<=n;i++)
if(sa[i-1]<la&&sa[i]>la||sa[i-1]>la&&sa[i]<la)
ans=max(ans,height[i]);
printf("%d\n",ans);
}
return 0;
}
后缀数组
不可重叠最长重复子串
题 意:有N(1 <= N <=20000)个音符的序列来表示一首乐曲,每个音符都是1..88范围内的整数,现在要找一个重复的主题。“主题”是整个音符序列的一个子串,它需要满足如下条件:
- 1.长度至少为5个音符。
- 2.在乐曲中重复出现。(可能经过转调,“转调”的意思是主题序列中每个音符都被加上或减去了同一个整数值)
- 3.重复出现的同一主题在原序列中不能有重叠部分。
思 路:假设是原序列的一个主题x1,x2,…,xn,经”转调”之后,该主题可能为x1+k,x2+k,…,xn+k,k∈Z+。 我们可以发现,一个主题,经“转调”后,与原序列不变的是相邻两音符的差值,即(xi+1+k)-(xi+k)=xi+1-xi。 故我们只需预处理出原序列中任意相邻音符的差值,就可以将问题转化为”不可重叠最长重复子串”,然后用后缀数组来做。
先二分答案,把题目变成判定性问题:判断是否存在两个长度为k的子串是相同的,且不重叠。解决这个问题的关键还是利用height数组。把排序后的后缀分成若干组,其中每组的后缀之间的height值都不小于k。例如,字符串为“aabaaaab”,当k=2时,后缀分成了4组,如图所示。
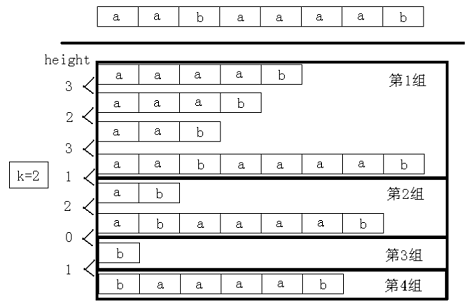 容易看出,有希望成为最长公共前缀不小于k的两个后缀一定在同一组。然后对于每组后缀,只须判断每个后缀的sa值的最大值和最小值之差是否不小于k。如果有一组满足,则说明存在,否则不存在。整个做法的时间复杂度为O(nlogn)。
容易看出,有希望成为最长公共前缀不小于k的两个后缀一定在同一组。然后对于每组后缀,只须判断每个后缀的sa值的最大值和最小值之差是否不小于k。如果有一组满足,则说明存在,否则不存在。整个做法的时间复杂度为O(nlogn)。
#include <bits/stdc++.h>
using namespace std;
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
const int N = 10;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
const int MAXN = 100010;
//rnk从0开始
//sa从1开始,因为最后一个字符(最小的)排在第0位
//height从1开始,因为表示的是sa[i - 1]和sa[i]
//倍增算法 O(nlogn)
int wa[MAXN], wb[MAXN], wv[MAXN], ws_[MAXN];
//Suffix函数的参数m代表字符串中字符的取值范围,是基数排序的一个参数,如果原序列都是字母可以直接取128,如果原序列本身都是整数的话,则m可以取比最大的整数大1的值
//待排序的字符串放在r数组中,从r[0]到r[n-1],长度为n
//为了方便比较大小,可以在字符串后面添加一个字符,这个字符没有在前面的字符中出现过,而且比前面的字符都要小
//同上,为了函数操作的方便,约定除r[n-1]外所有的r[i]都大于0,r[n-1]=0
//函数结束后,结果放在sa数组中,从sa[0]到sa[n-1]
void Suffix(int *r, int *sa, int n, int m){
int i, j, k, *x = wa, *y = wb, *t;
//对长度为1的字符串排序
//一般来说,在字符串的题目中,r的最大值不会很大,所以这里使用了基数排序
//如果r的最大值很大,那么把这段代码改成快速排序
for(i = 0; i < m; ++i) ws_[i] = 0;
for(i = 0; i < n; ++i) ws_[x[i] = r[i]]++;//统计字符的个数
for(i = 1; i < m; ++i) ws_[i] += ws_[i - 1];//统计不大于字符i的字符个数
for(i = n - 1; i >= 0; --i) sa[--ws_[x[i]]] = i;//计算字符排名
//基数排序
//x数组保存的值相当于是rank值
for(j = 1, k = 1; k < n; j *= 2, m = k){
//j是当前字符串的长度,数组y保存的是对第二关键字排序的结果
//第二关键字排序
for(k = 0, i = n - j; i < n; ++i) y[k++] = i;//第二关键字为0的排在前面
for(i = 0; i < n; ++i) if(sa[i] >= j) y[k++] = sa[i] - j;//长度为j的子串sa[i]应该是长度为2 * j的子串sa[i] - j的后缀(第二关键字),对所有的长度为2 * j的子串根据第二关键字来排序
for(i = 0; i < n; ++i) wv[i] = x[y[i]];//提取第一关键字
//按第一关键字排序 (原理同对长度为1的字符串排序)
for(i = 0; i < m; ++i) ws_[i] = 0;
for(i = 0; i < n; ++i) ws_[wv[i]]++;
for(i = 1; i < m; ++i) ws_[i] += ws_[i - 1];
for(i = n - 1; i >= 0; --i) sa[--ws_[wv[i]]] = y[i];//按第一关键字,计算出了长度为2 * j的子串排名情况
//此时数组x是长度为j的子串的排名情况,数组y仍是根据第二关键字排序后的结果
//计算长度为2 * j的子串的排名情况,保存到数组x
t = x;
x = y;
y = t;
for(x[sa[0]] = 0, i = k = 1; i < n; ++i)
x[sa[i]] = (y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + j] == y[sa[i] + j]) ? k - 1 : k++;
//若长度为2 * j的子串sa[i]与sa[i - 1]完全相同,则他们有相同的排名
}
}
int Rank[MAXN], height[MAXN], sa[MAXN], r[MAXN];
void calheight(int *r,int *sa,int n){
int i,j,k=0;
for(i=1; i<=n; i++)Rank[sa[i]]=i;
for(i=0; i<n; height[Rank[i++]]=k)
for(k?k--:0,j=sa[Rank[i]-1]; r[i+k]==r[j+k]; k++);
}
bool judge(int c,int n){
int Max=sa[0],Min=sa[0];
for(int i=1;i<n;i++){
if(height[i]>=c)
Max=max(Max,sa[i]),Min=min(Min,sa[i]);
else
Max=sa[i],Min=sa[i];
if(Max-Min>=c+1)
return true;
}
return false;
}
int main(){
int n,i,Max=0,L,R,mid,ans;
while(~scanf("%d",&n)&&n){
for(i=0;i<n;i++){
scanf("%d",&r[i]);
if(i)
r[i-1]=r[i]-r[i-1]+88;
Max=max(Max,r[i-1]);
}
r[i-1]=0;n--;
Suffix(r,sa,n+1,Max+1);
calheight(r,sa,n);
L=0;R=n;ans=0;
while(L<=R){
mid=(L+R)/2;
if(judge(mid,n+1))
L=mid+1,ans=max(ans,mid);
else
R=mid-1;
}
if(ans<4)
puts("0");
else
printf("%d\n",ans+1);
}
return 0;
}
树状结构
二叉查找树(Binary Search Tree,简称为BST),有时也被翻译为二叉搜索树或二叉排序树。在很多情况下可以良好的工作,但它的限制是最坏情况下的渐进运行时间为 O(n)。
二叉查找树递归定义如下:
- 要么是一棵空树
- 如果不为空,那么其左子树节点的值都小于根节点的值;右子树节点的值都大于根节点的值
- 其左右子树也是二叉查找树
中序遍历二叉排序树可得到一个关键字的有序序列,一个无序序列可以通过构造一棵二叉排序树变成一个有序序列,构造树的过程也可以看成是对无序序列进行排序的过程。
普通的二叉搜索树存在的问题:
- 考虑一组本来就有序的数列,将其插入二叉搜索树,结果就是二叉树会退化成一条链,所有结点只有右子树,左子树是空的。因而预期的O(logn)的操作会退化成O(n)。
平衡查找树(Balanced Search Tree)的设计则是保证其高度在最坏的情况下为 O(log n),其插入、删除和查找可以实现渐进运行时间 O(log n)。
平衡二叉树递归定义如下:
- 其每一个子树均为平衡二叉树
- 左右子树的高度差小于等于 1
现在其实存在很多种类的平衡查找树,常见的有 AVL树、红黑树、B 树等,不同的平衡查找树的高度(height):
- AVL 树:高度 ≤ (1.44042..)log2 n
- 红黑树:高度 ≤ 2*log2 (n+1)
- 2-3 树:高度 ≤ log2 n
- 2-3-4 树:高度 ≤ log2 n
AVL 平衡二叉树
AVL树是一种平衡二叉树,1962年由两位俄罗斯的数学家Adelson-Velskii和Landis提出。
AVL树的定义:
- 它的左子树和右子树都是AVL树
- 左子树和右子树的高度差不能超过1
AVL树的性质:
- 一棵n个结点的AVL树的其高度保持在0(log2(n)),不会超过3/2log2(n+1)
- 一棵n个结点的AVL树的平均搜索长度保持在0(log2(n)).
- 一棵n个结点的AVL树删除一个结点做平衡化旋转所需要的时间为0(log2(n)).
题 意:题意定义了四种操作:
- 1表示有一个编号为k的顾客进入等待的队列,他的优先度为p。
- 2处理优先度最高的顾客,并从等待队列中清除,输出其编号,队列为空输出0。
- 3处理优先度最低的顾客,并从等待队列中清除,输出其编号,队列为空输出0。
- 0表示操作结束。
思 路:AVL树模板题,对于输入的client,按照优先度建立二叉查找树,在需要输出的时候,将对应的节点提到根节点,然后将其删掉。
#include <bits/stdc++.h>
using namespace std;
#define MAX(x, y) ((x)>(y)?(x):(y))
typedef struct NODE{
int val, data;
int bf; //平衡因子(左子树高度与右子树高度之差)
int h; //以当前结点为根结点的数的高度
NODE *l, *r;
}Node;
class BalanceTree{
public:
void Init(){
rt = NULL;
}
int Height(Node *T){
if(NULL == T) return 0;
return T->h;
}
int BF(Node *l, Node *r){
if(NULL == l && NULL == r) return 0;
else if(NULL == l) return -r->h;
else if(NULL == r) return l->h;
else return l->h - r->h;
}
Node *LL_rotate(Node *A){
Node *B;
B = A->l;
A->l = B->r;
B->r = A;
A->h = MAX(Height(A->l), Height(A->r)) + 1;
B->h = MAX(Height(B->l), Height(B->r)) + 1;
A->bf = BF(A->l, A->r);
B->bf = BF(B->l, B->r);
return B;
}
Node *RR_rotate(Node *A){
Node *B;
B = A->r;
A->r = B->l;
B->l = A;
A->h = MAX(Height(A->l), Height(A->r)) + 1;
B->h = MAX(Height(B->l), Height(B->r)) + 1;
A->bf = BF(A->l, A->r);
B->bf = BF(B->l, B->r);
return B;
}
Node *LR_rotate(Node *A){
Node *C;
A->l = RR_rotate(A->l);
C = LL_rotate(A);
return C;
}
Node *RL_rotate(Node *A){
Node *C;
A->r = LL_rotate(A->r);
C = RR_rotate(A);
return C;
}
void Insert(int v, int e){
Insert_(rt, v, e);
}
void Insert_(Node *&T, int v, int e){
if(NULL == T){
T = (Node *)malloc(sizeof(Node));
T->val = v;
T->data = e;
T->bf = 0;
T->h = 1;
T->l = T->r = NULL;
return;
}
if(e < T->data) Insert_(T->l, v, e);
else Insert_(T->r, v, e);
T->h = MAX(Height(T->l), Height(T->r)) + 1;
T->bf = BF(T->l, T->r);
if(T->bf > 1 || T->bf < -1){ //T结点失衡
if(T->bf > 0 && T->l->bf > 0) T = LL_rotate(T); //如果T->bf > 0 则肯定有左儿子
else if(T->bf < 0 && T->r->bf < 0) T = RR_rotate(T); //如果T->bf < 0 则肯定有右儿子
else if(T->bf > 0 && T->l->bf < 0) T = LR_rotate(T);
else if(T->bf < 0 && T->r->bf > 0) T = RL_rotate(T);
}
}
void Delete(int flag){ //flag为1表示找最大值
if(NULL == rt){
printf("0\n");
return;
}
Node *tmp = rt;
if(!flag) while(tmp->l) tmp = tmp->l;
else while(tmp->r) tmp = tmp->r;
printf("%d\n", tmp->val);
Delete_(rt, tmp->data);
}
void Delete_(Node *&T, int key){
if(NULL == T) return;
if(key < T->data){ //从左边删除
Delete_(T->l, key);
T->bf = BF(T->l, T->r); //计算删除后T结点的平衡因子
if(T->bf < -1){ //T结点左边高度变小(删了左边的元素)导致失衡
if(1 == T->r->bf) T = RL_rotate(T); //RL型
else T = RR_rotate(T); //平衡因子为0或-1
}
}
else if(key > T->data){ //从右边删除
Delete_(T->r, key);
T->bf = BF(T->l, T->r); //计算删除后T结点的平衡因子
if(T->bf > 1){ //T结点右边高度变小(删了右边的元素)导致失衡
if(-1 == T->l->bf) T = LR_rotate(T); //LR型
else T = LL_rotate(T); //平衡因子为0或1
}
}
else{
if(T->l && T->r){ //左右都不为空
Node *tmp = T;
while(tmp->r) tmp = tmp->r;
T->data = tmp->data;
Delete_(T->l, tmp->data);
T->bf = BF(T->l, T->r); //计算删除后T结点的平衡因子
if(T->bf < -1){ //T结点左边高度变小(删了左边的元素)导致失衡
if(1 == T->r->bf) T = RL_rotate(T); //RL型
else T = RR_rotate(T); //平衡因子为0或-1
}
}
else{
Node *tmp = T;
if(T->l) T = T->l; //有左儿子
else if(T->r) T = T->r; //有右儿子
else{ //T无儿子
free(T);
T = NULL;
}
if(T) free(tmp);
}
}
}
void Show(){
InOrder(rt);
printf("\n");
}
void InOrder(Node *T){
if(NULL == T) return;
InOrder(T->l);
printf("%d(%d) ", T->val, T->data);
InOrder(T->r);
}
void Free(){
FreeTree(rt);
}
void FreeTree(Node *T){
if(NULL == T) return;
FreeTree(T->l);
FreeTree(T->r);
free(T);
}
private:
Node *rt;
};
BalanceTree bt;
int main(){
//freopen("in.txt","r",stdin);
int op, v, e;
bt.Init();
while(scanf("%d", &op), op){
if(1 == op){
scanf("%d%d", &v, &e);
bt.Insert(v, e);
}
else if(2 == op)
bt.Delete(1);
else if(3 == op)
bt.Delete(0);
}
bt.Free();
return 0;
}
Splay Tree 伸展树
Splay其实并不是一棵严格意义上的平衡树,因为它的操作并不是主要为了保证左右平衡的,它的特点主要是结构比较灵活,可以用来处理一些正常平衡树完成不了的问题(缺点就是常数大,效率可能不高)。
Splay树核心过程:Splay(x, y),即将x节点转移到y节点的子节点上面(其中y是x的祖先)。利用其中双旋的优势能够保证查询复杂度均摊为O(log n)。
一开始理解有些困难,其实实际上不做深入的理解就是,双旋的过程就是一个建立相对平衡的二叉树的一个过程。
对于二叉树,最极端的情况就是线性插入,使得整棵二叉树退化为一条链。比如你查询链的最后一个节点,之后再次查询第一个节点。
- 1)若只是单旋通过Splay(x, 0)将最后一个节点移动到根节点,需要O(n)复杂度,而查询第一个节点时又需要O(n)复杂度,来来往往就退化成一条链了。
- 2)若是双旋Splay(x, 0)将最后一个节点移动到根节点上时,移动过程中建立起了相对平衡的二叉树,需要O(n),也就是查询第一个节点时,大概是需要O(lgn)复杂度。这就降低了复杂度。可以证明,总的每个操作的均摊复杂度是O(lgn)。
具体证明可以参见杨思雨《伸展树的基本操作与应用》
题 意:给出五种操作:
- ADD x y D: 对区间[x,y]全部加上D;
- REVERSE x y: 反转区间[x,y];
- REVOLVE x y T: 将区间[x,y]向右循环平移T次,每次一格,例如 REVOLVE 2 4 2 在{1, 2, 3, 4, 5}操作结果为{1, 3, 4, 2, 5};
- INSERT x P: 在位置x后面插入一个数P;
- DELETE x: 删除位置x上的数;
- MIN x y: 求区间[x,y]中的最小值;
思 路:splay模板题,lazy标记模仿线段树标记区间加上多少,rev标记标记是否需要反转,mini[x]记录节点x统领的整棵子树(包含自己)的key[x]的最小值。
#include <bits/stdc++.h>
using namespace std;
#define Key_value ch[ch[root][1]][0]
const int maxn=2e5+10;
int n,m;
int a[maxn];
int root,nodecnt;
int par[maxn],ch[maxn][2];
int key[maxn],mini[maxn],size[maxn];
int lazy[maxn]; //lazy标记
bool rev[maxn]; //反转标记
int pool[maxn],poolsize; //节点回收
void NewNode(int &x,int p,int k){
if(poolsize>0) x=pool[--poolsize];
else x=++nodecnt;
par[x]=p;
ch[x][0]=ch[x][1]=0;
key[x]=k;
mini[x]=k;
size[x]=1;
lazy[x]=0;
rev[x]=0;
}
void Update_Rev(int x){
if(x==0) return;
swap(ch[x][0],ch[x][1]);
rev[x]^=1;
}
void Update_Add(int x,int val){
if(x==0) return;
key[x]+=val;
mini[x]+=val;
lazy[x]+=val;
}
void Pushup(int x){
size[x]=size[ch[x][0]]+size[ch[x][1]]+1;
mini[x]=key[x];
if(ch[x][0]) mini[x]=min(mini[x],mini[ch[x][0]]);
if(ch[x][1]) mini[x]=min(mini[x],mini[ch[x][1]]);
}
void Pushdown(int x){
if(rev[x])
{
Update_Rev(ch[x][0]);
Update_Rev(ch[x][1]);
rev[x]=0;
}
if(lazy[x])
{
Update_Add(ch[x][0],lazy[x]);
Update_Add(ch[x][1],lazy[x]);
lazy[x]=0;
}
}
void Inorder(int x){ //debug
if(x==0) return;
Pushdown(x);
Inorder(ch[x][0]);
printf("%d ",key[x]);
Inorder(ch[x][1]);
Pushup(x);
if(x==root) printf("\n");
}
void Rotate(int x,int type){ //旋转,0为左旋zag,1为右旋zig
int y=par[x];
Pushdown(y); Pushdown(x); //先把y的标记向下传递,再把x的标记往下传递
ch[y][!type]=ch[x][type]; par[ch[x][type]]=y;
if(par[y]) ch[par[y]][(ch[par[y]][1]==y)]=x;
par[x]=par[y];
ch[x][type]=y; par[y]=x;
Pushup(y); Pushup(x);
}
void Splay(int x,int goal){
while(par[x]!=goal){
if(par[par[x]]==goal) Rotate(x,ch[par[x]][0]==x); //左孩子zig,右孩子zag
else{
Pushdown(par[par[x]]); Pushdown(par[x]); Pushdown(x);
int y=par[x];
int type=(ch[par[y]][0]==y); //type=0,y是右孩子;type=1,y是左孩子
if(ch[y][type]==x){
Rotate(x,!type);
Rotate(x,type);
}
else{
Rotate(y,type);
Rotate(x,type);
}
}
}
if(goal==0) root=x;
}
int Get_Kth(int x,int k){ //得到第k个节点
Pushdown(x);
int t=size[ch[x][0]]+1;
if(t==k) return x;
if(t>k) return Get_Kth(ch[x][0],k);
else return Get_Kth(ch[x][1],k-t);
}
int Get_Min(int x){
Pushdown(x);
while(ch[x][0]){
x=ch[x][0];
Pushdown(x);
}
return x;
}
int Get_Max(int x){
Pushdown(x);
while(ch[x][1]){
x=ch[x][1];
Pushdown(x);
}
return x;
}
void Build(int &x,int l,int r,int par){ //建树,先建立中间结点,再建两端的方法
if(l>r) return;
int mid=(l+r)/2;
NewNode(x,par,a[mid]);
Build(ch[x][0],l,mid-1,x);
Build(ch[x][1],mid+1,r,x);
Pushup(x);
}
void Init(){ //初始化,前后各加一个空节点
root=nodecnt=poolsize=0;
par[root]=ch[root][0]=ch[root][1]=0;
key[root]=size[root]=0;
lazy[root]=rev[root]=0;
NewNode(root,0,-1); //头部加入一个空位
NewNode(ch[root][1],root,-1); //尾部加入一个空位
Build(Key_value,1,n,ch[root][1]);
Pushup(ch[root][1]);
Pushup(root);
}
void Add(int l,int r,int val){
Splay(Get_Kth(root,l-1+1),0); //l的前驱l-1伸展到根
Splay(Get_Kth(root,r+1+1),root); //r的后继r+1伸展到根的右孩子
Update_Add(Key_value,val);
Pushup(ch[root][1]);
Pushup(root);
}
void Move(int l,int r,int p){ //截取[l,r]放到位置p之后
Splay(Get_Kth(root,l-1+1),0); //l的前驱l-1伸展到根
Splay(Get_Kth(root,r+1+1),root); //r的后继r+1伸展到根的右孩子
int tmp=Key_value; //Key_value=ch[ch[root][1]][0]所统领的子树即[l,r]
Key_value=0; //剥离[l,r]子树
Pushup(ch[root][1]); Pushup(root);
Splay(Get_Kth(root,p+0+1),0); //p伸展到根
Splay(Get_Kth(root,p+1+1),root); //p的后继p+1伸展到根的右孩子
Key_value=tmp; par[Key_value]=ch[root][1]; //接上[l,r]子树
Pushup(ch[root][1]); Pushup(root);
}
void Reverse(int l,int r){ //反转[l,r]区间
Splay(Get_Kth(root,l-1+1),0);
Splay(Get_Kth(root,r+1+1),root);
Update_Rev(Key_value);
Pushup(ch[root][1]);
Pushup(root);
}
void Revolve(int l,int r,int T){
int D=r-l+1;
int L=T%D;
if(L==0) return;
Move(r-L+1,r,l-1);
}
void Insert(int p,int k){
Splay(Get_Kth(root,p+0+1),0); //p伸展到根
Splay(Get_Kth(root,p+1+1),root); //p的后继p+1伸展到根的右孩子
Inorder(Key_value);
NewNode(Key_value,ch[root][1],k);
Pushup(ch[root][1]); Pushup(root);
}
void Collect(int x){ //回收节点x统领的子树
if(x==0) return;
pool[poolsize++]=x;
Collect(ch[x][0]);
Collect(ch[x][1]);
}
void Delete(int p){
Splay(Get_Kth(root,p-1+1),0); //p的前驱p-1伸展到根
Splay(Get_Kth(root,p+1+1),root); //p的后继p+1伸展到根的右孩子
Collect(Key_value);
par[Key_value]=0;
Key_value=0;
Pushup(ch[root][1]); Pushup(root);
}
int Min(int l,int r){
Splay(Get_Kth(root,l-1+1),0);
Splay(Get_Kth(root,r+1+1),root);
return mini[Key_value];
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
Init();
scanf("%d",&m);
char op[50];
for(int i=1;i<=m;i++){
scanf("%s",op);
if(op[0]=='A'){
int x,y,D; scanf("%d%d%d",&x,&y,&D);
Add(x,y,D);
}
if(op[0]=='R' && op[3]=='E'){
int x,y; scanf("%d%d",&x,&y);
Reverse(x,y);
}
if(op[0]=='R' && op[3]=='O'){
int x,y,T; scanf("%d%d%d",&x,&y,&T);
Revolve(x,y,T);
}
if(op[0]=='I'){
int x,p; scanf("%d%d",&x,&p);
Insert(x,p);
}
if(op[0]=='D'){
int x; scanf("%d",&x);
Delete(x);
}
if(op[0]=='M'){
int x,y; scanf("%d%d",&x,&y);
printf("%d\n",Min(x,y));
}
//Inorder(root);
}
return 0;
}
Treap 树堆
AVL树、伸展树的主要问题就是其结构与数据相关,树的深度可能会很大,Treap树就是一种解决二叉搜索树深度过大的一种数据结构。
Treap是用优先级的思想,在树上加上堆(Treap=Tree+Heap)。每个节点多了一个优先级fix,对于每个节点,该节点的优先级小于等于其所有孩子的优先级。
#include <bits/stdc++.h>
using namespace std;
typedef struct TreapNode* Tree;
typedef int ElementType;
struct TreapNode{
ElementType val; //结点值
int priority; //优先级
Tree lchild;
Tree rchild;
TreapNode(int val=0,int priority=0){ //默认构造函数
lchild=rchild=NULL;
this->val=val;
this->priority=priority;
}
};
Tree search(Tree &,ElementType);
void right_rotate(Tree &);
void left_rotate(Tree &);
bool insert_val(Tree &,Tree &);
bool insert(Tree &,ElementType,int);
bool remove(Tree &,ElementType);
//查找函数
Tree search(Tree &root,ElementType val){
if (!root)
return NULL;
else if (root->val>val)
return search(root->lchild,val);
else if(root->val<val)
return search(root->rchild,val);
return root;
}
//插入函数
bool insert(Tree &root,ElementType val=0,int priority=0){
Tree node=new TreapNode(val,priority);
return insert_val(root, node);
}
//内部插入函数(参数:根结点,需插入的结点)
bool insert_val(Tree &root,Tree &node){
if (!root){
root=node; //插入
return true;
}
else if(root->val>node->val){
bool flag=insert_val(root->lchild, node);
if (root->priority>node->priority) //检查是否需要调整
right_rotate(root);
return flag;
}
else if(root->val<node->val){
bool flag=insert_val(root->rchild, node);
if (root->priority>node->priority) //检查是否需要调整
left_rotate(root);
return flag;
}
//已经含有该元素,释放结点
delete node;
return false;
}
//右旋转
void right_rotate(Tree &node){
Tree temp=node->lchild;
node->lchild=temp->rchild;
temp->rchild=node;
node=temp;
}
//左旋转
void left_rotate(Tree &node){
Tree temp=node->rchild;
node->rchild=temp->lchild;
temp->lchild=node;
node=temp;
}
//删除函数
bool remove(Tree &root,ElementType val){
if (root==NULL)
return false;
else if (root->val>val)
return remove(root->lchild,val);
else if(root->val<val)
return remove(root->rchild,val);
else{ //找到执行删除处理
Tree *node=&root;
while ((*node)->lchild && (*node)->rchild){ //从该结点开始往下调整
if ((*node)->lchild->priority<(*node)->rchild->priority){ //比较其左右孩子优先级
right_rotate(*node); //右旋转
node=&((*node)->rchild); //更新传入参数,进入下一层
}
else{
left_rotate(*node); //左旋转
node=&((*node)->lchild); //更新传入参数,进入下一层
}
}
//最后调整到(或者本来是)叶子结点,或者只有一个孩子的情况,可以直接删除了
if ((*node)->lchild==NULL)
(*node)=(*node)->rchild;
else if((*node)->rchild==NULL)
(*node)=(*node)->lchild;
return true;
}
}
//前序
void PreOrder(Tree root){
if (root==NULL)
return;
printf("%d ",root->val);
PreOrder(root->lchild);
PreOrder(root->rchild);
}
//中序
void InOrder(Tree root){
if (root==NULL)
return;
InOrder(root->lchild);
printf("%d ",root->val);
InOrder(root->rchild);
}
int main(){
Tree root=NULL;
insert(root,11,6);
insert(root,7,13);
insert(root,14,14);
insert(root,3,18);
insert(root,9,22);
insert(root,18,20);
insert(root,16,26);
insert(root,15,30);
insert(root,17,12);
printf("插入:\n");
printf("前序:");
PreOrder(root);
printf("\n");
printf("中序:");
InOrder(root);
printf("\n");
printf("删除:\n");
remove(root,11);
printf("前序:");
PreOrder(root);
printf("\n");
printf("中序:");
InOrder(root);
printf("\n");
return 0;
}
Cartesian Tree 笛卡尔树
笛卡尔树跟Treap几乎是一模一样的,只是用途不同。笛卡尔树是把已有的一些(key, fix)二元组拿来构造树,然后利用构树过程和构造好的树来解决LCA、RMQ等等问题。
题 意:给出一个n,在给出n对数(且命名为x,y),构建一棵树,满足以下条件:
- 对树上任意一个节点,有x > leftson_x 且x > rigthson_x
- 对树上任意一个节点,有y > father_y
构建完成后,输出每个点的父节点,左子节点,右子节点,没有的以0代替。
思 路:笛卡尔树模板题,笛卡尔树每个节点有两个值,且称为val和pri,满足以下条件:
- 满足任意节点的val,大于其左子节点的val,小于其右子节点的val。
- 满足任意节点的pri,要么全部小于其父节点的pri,要么全部大于其父节点的pri,视题目有所不同,此题是第二种情况。
可以在O(n)的时间内构建一颗笛卡尔树(此处按pri的第二种情况建树)。首先对所有节点按val从小到大排序,然后维护一个单调栈,栈中元素的pri从栈底到栈顶依次递增,这个栈实际上维护的是树的最右链,每次有新元素加入时,从栈顶向栈底遍历,栈中元素的pri大于新元素的pri的话,就直接出栈,直到遇到栈中一个元素的pri小于新元素的pri,那么把这个新元素挂到这个栈中元素的右儿子上,把刚刚出栈的最后一个元素挂到新元素的左儿子上,可以发现这样是满足建树的条件1。就这样一直进行下去,到最后,栈底的元素就是笛卡尔树的树根。
此题用treap会TLE。
#include <bits/stdc++.h>
using namespace std;
const int N = 50000 + 10, INF = 0x3f3f3f3f;
int root;
struct node{
int val, pri, fat, id, son[2];
friend bool operator< (node a, node b){
return a.val < b.val;
}
void init(int _val, int _pri, int _fat, int _id){
val = _val, pri = _pri, fat = _fat, id = _id;
son[0] = son[1] = 0;
}
}tr[N];
int stk[N], top;
int ans_fat[N], ans_l[N], ans_r[N];
int cartesian_build(int n){
top = 0;
for(int i = 1; i <= n; i++){
int k = top;
while(k > 0 && tr[stk[k-1]].pri > tr[i].pri) k--;//栈中元素的pri大于新元素的pri就直接出栈
if(k != 0){ //栈中还有元素,就把新元素挂到这个元素的右儿子上
tr[i].fat = stk[k-1];
tr[stk[k-1]].son[1] = i;
//ans_fat[tr[i].id] = tr[stk[k-1]].id; //注释的这些去掉就不用dfs了,只不过为了熟悉笛卡尔树所以又写了个dfs求答案
//ans_r[tr[stk[k-1]].id] = tr[i].id;
}
if(k != top){ //有元素出栈,则把出栈的最后一个元素挂到新元素的左儿子上
tr[stk[k]].fat = i;
tr[i].son[0] = stk[k];
//ans_fat[tr[stk[k]].id] = tr[i].id;
//ans_l[tr[i].id] = tr[stk[k]].id;
}
stk[k++] = i;
top = k;
}
return stk[0];
}
void dfs(int x, int fat){
if(! x) return;
ans_fat[tr[x].id] = tr[fat].id;
ans_l[tr[x].id] = tr[tr[x].son[0]].id;
ans_r[tr[x].id] = tr[tr[x].son[1]].id;
dfs(tr[x].son[0], x);
dfs(tr[x].son[1], x);
}
int main(){
int n;
while(~ scanf("%d", &n)){
int a, b;
tr[0].init(0, 0, 0, 0);
for(int i = 1; i <= n; i++){
scanf("%d%d", &a, &b);
tr[i].init(a, b, 0, i);
}
sort(tr + 1, tr + 1 + n);
root = cartesian_build(n);
dfs(root, 0);
puts("YES");
for(int i = 1; i <= n; i++) printf("%d %d %d\n", ans_fat[i], ans_l[i], ans_r[i]);
}
return 0;
}
2-3-4树
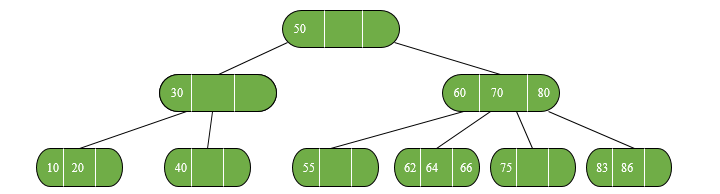
2-3-4树是平衡树,但不是二叉树,因为它可以有多个节点值,也可以有多个节点。在计算机科学中是阶为4的B树,其名字是根据子节点数来确定的,它可以实现完美平衡:
2-3-4树的key的种类:
2-node: 一个key值,两个儿子节点。
3-node: 两个key值,三个儿子节点。
4-node: 三个key值,四个儿子节点。
RB-tree 红黑树
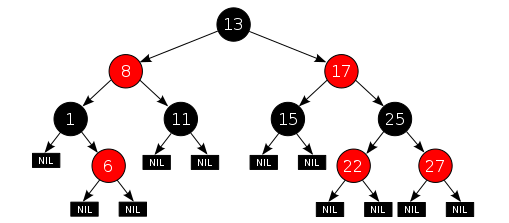
AVL 树是高度平衡的,频繁的插入和删除,会引起频繁的reblance,导致效率下降。
红黑树不是高度平衡的,算是一种折中(插入最多两次旋转,删除最多三次旋转):
- 吸收了2-3-4树和AVL树的优点,放弃了AVL树完美平衡的特性,改为局部平衡和完美黑色平衡。
- 放弃2-3-4树的多节点,改为使用颜色来区分不同的节点类型。这样就降低了维护的成本和时间复杂度。可以直接使用二叉排序树的查找方法来进行查找操作。
红黑树的定义:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
因此,红黑树在很多地方都有应用。在C++ STL中,很多部分(目前包括 set, multiset, map, multimap)应用了红黑树的变体。SGI STL中的红黑树有一些变化,这些修改提供了更好的性能,以及对set操作的支持。
SBT 节点大小平衡树
节点大小平衡树(Size Balanced Tree)是一种自平衡二叉查找树,由中国广东中山纪念中学的陈启峰(也是个神人,本来那年拿到了北美地区的ACM冠军,结果封神之路上遇到了Watashi)发明的。陈启峰于2006年底完成论文《Size Balanced Tree》,并在2007年的全国青少年信息学奥林匹克竞赛冬令营中发表。
相比红黑树、AVL树等自平衡二叉查找树,SBT更易于实现。据陈启峰在论文中称,SBT是“目前为止速度最快的高级二叉搜索树”。
题 意:给定了初始的状态:有n个村庄连成一条直线,现在有三种操作: 1.摧毁一个村庄 2.询问某个村庄,输出与该村庄相连的村庄数量(包括自己) 3.修复被摧毁的村庄,优先修复最近被摧毁的…………..
分 析:用SBT做的话,摧毁村庄就插入,修复就移除,如果要询问的话:找到第一个大于等于该村庄编号和第一个小于等于该村庄编号的,等价于找到了联通在一起的村庄。
思 路:SBT + stack + 二分
#include <bits/stdc++.h>
using namespace std;
struct sbt {
int l,r,s,key;
} tr[MAX];
int top , root;
void left_rot(int &x) {
int y = tr[x].r;
tr[x].r = tr[y].l;
tr[y].l = x;
tr[y].s = tr[x].s; //转上去的节点数量为先前此处节点的size
tr[x].s = tr[tr[x].l].s + tr[tr[x].r].s + 1;
x = y;
}
void right_rot(int &x) {
int y = tr[x].l;
tr[x].l = tr[y].r;
tr[y].r = x;
tr[y].s = tr[x].s;
tr[x].s = tr[tr[x].l].s + tr[tr[x].r].s + 1;
x = y;
}
void maintain(int &x,bool flag) {
if(flag == 0) { //左边
if(tr[tr[tr[x].l].l].s > tr[tr[x].r].s) {//左孩子左子树size大于右孩子size
right_rot(x);
} else if(tr[tr[tr[x].l].r].s > tr[tr[x].r].s) {//左孩子右子树size大于右孩子size
left_rot(tr[x].l);
right_rot(x);
} else return ;
} else { //右边
if(tr[tr[tr[x].r].r].s > tr[tr[x].l].s) { //右孩子的右子树大于左孩子
left_rot(x);
} else if(tr[tr[tr[x].r].l].s > tr[tr[x].l].s) { //右孩子的左子树大于左孩子
right_rot(tr[x].r);
left_rot(x);
} else return ;
}
maintain(tr[x].l,0);
maintain(tr[x].r,1);
}
void insert(int &x,int key) {
if(x == 0) { //空节点
x = ++ top;
tr[x].l = tr[x].r = 0;
tr[x].s = 1;
tr[x].key = key;
} else {
tr[x].s ++;
if(key < tr[x].key) insert(tr[x].l,key);
else insert(tr[x].r,key);
maintain(x,key >= tr[x].key);
}
}
int remove(int &x,int key) {
int k;
tr[x].s --;
if(key == tr[x].key || (key < tr[x].key && tr[x].l == 0) || (key > tr[x].key && tr[x].r == 0)) {
k = tr[x].key;
if(tr[x].l && tr[x].r) {
tr[x].key = remove(tr[x].l,tr[x].key + 1);
} else {
x = tr[x].l + tr[x].r;
}
} else if(key > tr[x].key) {
k = remove(tr[x].r,key);
} else if(key < tr[x].key) {
k = remove(tr[x].l,key);
}
return k;
}
int pred(int &x,int y,int key){ //前驱 小于
if(x == 0) return tr[y].key ;
if(tr[x].key < key) return pred(tr[x].r,x,key);
else if(tr[x].key > key) return pred(tr[x].l,y,key);
else return key;
}
//pred(root,0,key)
int succ(int &x,int y,int key) { //后继 大于
if(x == 0) return tr[y].key;
if(tr[x].key > key) return succ(tr[x].l,x,key);
else if(tr[x].key < key) return succ(tr[x].r,y,key);
else return key;
}
int n,m;
char c;
int st[MAX];
int head = 0;
int main() {
root = 0;
top = 0;
int b;
scanf("%d%d",&n,&m);
for(int i=0; i<m; i++) {
cin >> c;
if(c == 'D') {
scanf("%d",&b);
st[head++] = b;
insert(root,b);
}
if(c == 'R') {
remove(root,st[--head]);
}
if(c == 'Q') {
scanf("%d",&b);
int pre = pred(root,0,b);
int suc = succ(root,0,b);
if(suc == 0) suc = n+1;
if(pre == suc) {
puts("0");
continue;
}
printf("%d\n",suc - pre - 1);
}
}
return 0;
}
堆型结构
堆的性质:任意节点的关键字大于等于其孩子节点的关键字(小顶堆)。
- 堆性质是为了让最小的结点始终在根的位置,这是所有堆都有的性质。
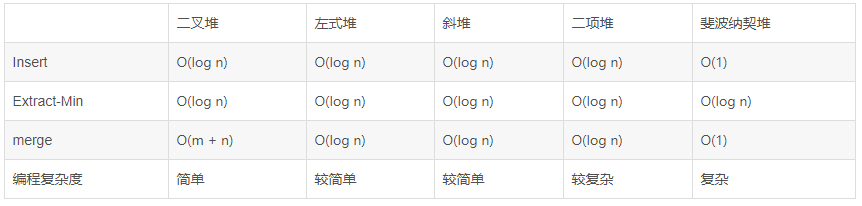
以上都是可合并堆(Mergeable Heap)。其中二项堆(使用孩子兄弟存储模式)和斐波纳契堆(使用树型结构配合双向循环链表模式)由于编程的复杂性和比较大的常数因子,所以使用的很少。
Leftist Tree 左偏堆
最常用的一种可合并堆。
左偏堆(树)的性质:定义到最近的孩子的距离为节点距离dist,那么任意节点的左孩子的距离大于右孩子的距离。
- A->lchild->dist >= A->rchild->dist
左偏性质是为了让树状存储的堆,树的深度不能过大,且利于合并。左偏性质使树的左侧的深度始终大于等于右侧的深度:
- 在实现插入操作时总是从右侧插入,也就是总是让短的一侧生长,如果右侧长于了左侧,那么把左右侧交换一下,继续从短的一侧生长。
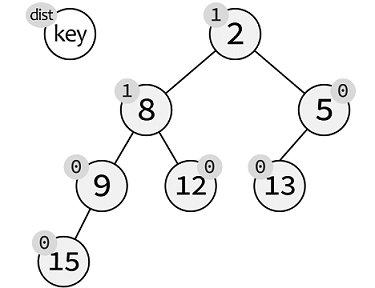
节点的距离的定义:
- 某个节点被称为外节点,仅当这个节点的左子树或右子树为空。某一个节点的距离即该节点到与其最近的外节点经过的边数。易得,外节点的距离为0,空节点距离为−1。特别的,我们把根结点的距离称为这棵左偏树的距离。
左偏堆(树)merge函数具体实现:
- 采用递归实现
- 每层递归中, 当roota->val > rootb->val时, 交换roota和rootb
- 向下递归
- 如左子节点距离小于右子节点距离, 交换左右子节点
- 更新本节点距离值
- 返回本节点指针
题 意:给出一串数,改变当个数字的大小的代价是改动的绝对值(比如2变成5,代价是3),求让这个数串变成非递减(或非递增)数列的最小代价。
分 析:对于一个非递减序列,最小代价是把每个数都变成这个序列的中位数。
思 路:用左边树保存每一段部分的中位数。把每个数单独建一颗左偏树。因为只有一个数,当然中位数是自己。 树里面只保存(len+1)/2个节点,len为这课左偏树所管理的长度(即影响范围)。然后从左往右扫,一旦扫到后面的中位数比前面的中位数要小,就把这两棵树合并。
#include <bits/stdc++.h>
using namespace std;
#define MAXN 2010
#define LL long long
#define min(a, b) (a < b ? a : b)
struct Node{
int v, l, r, dis;
Node() {}
Node(int _v, int _l, int _r, int _d):
v(_v), l(_l), r(_r), dis(_d) {}
}nn[2][MAXN];
int merge(Node n[], int x, int y){
if(!x) return y;
if(!y) return x;
if(n[x].v < n[y].v) swap(x, y);
n[x].r = merge(n, n[x].r, y);
if(n[n[x].l].dis < n[n[x].r].dis) swap(n[x].l, n[x].r);
n[x].dis = n[n[x].r].dis + 1;
return x;
}
int N, v[MAXN], len[MAXN], stk[MAXN];
LL ans[2];
void solve(Node n[], int t){
int top = 0;
for(int i = 0; i < N; i++){
int ct = 1; int id = i;
while(top > 0 && n[stk[top - 1]].v > n[id].v){
top--;
id = merge(n, stk[top], id);
if((len[top] + 1) / 2 + (ct + 1) / 2 > (len[top] + ct + 1) / 2)
id = merge(n, n[id].l, n[id].r);
ct += len[top];
}
len[top] = ct;
stk[top++] = id;
}
for(int i = 0, j = 0; i < top; i++){
int k = n[stk[i]].v;
while(len[i]--) ans[t] += abs(v[j++] - k);
}
}
int main(){
while(~scanf("%d", &N)){
memset(len, 0, sizeof(len));
memset(nn, 0, sizeof(nn));
for(int i = 0; i < N; i++){
scanf("%d", &v[i]);
nn[0][i] = nn[1][N - i + 1] = Node(v[i], 0, 0, 0);
}
ans[0] = ans[1] = 0;
for(int i = 0; i < 2; i++) solve(nn[i], i);
printf("%I64d\n", min(ans[0], ans[1]));
}
return 0;
}
Skew Heap 斜堆
斜堆(Skew Heap)也叫自适应堆(self-adjusting heap),是一种使用二叉树实现的堆状数据结构。斜堆的优势是其合并的速度远远大于二叉堆。斜堆是一种自适应的左偏树。
斜堆的性质:
- 本节点的键值key小于其左右子节点键值key
- 斜堆节点不存储距离dist值, 取而代之的是在每次合并操作时都做swap处理(节省了存储空间)
斜堆merge函数具体实现:
- 采用递归实现(也有非递归算法)
- 每层递归中, 当roota->val > rootb->val时, 交换roota和rootb
- 向下递归
- 交换左右子节点
- 返回本节点指针
题 意: 有 n 只猴子,每只猴子都有一个力量,开始时互相都不认识,它们之间发生 m 次争斗,每次a和b发生争斗时,a和b会从它们认识的猴子中选出一个最强的,并变为这两只猴子发生争斗,打完之后这两个猴子就互相认识,并且力量减半,如果a和b互相认识就输出−1,否则输出认识的猴子中最大的力量值。
思 路:并查集+可并堆(这里用了斜堆,左斜堆也可以)。
先将每个节点看成是一个堆,然后使用并查集来查询当前输入的两个节点的父节点,如果两个节点的父节点相同,则表明两个猴子在一个群体中,直接输出-1,否则使用斜堆将每个堆的堆顶元素的值更新(先删除堆顶元素,然后再插入一个值为原来堆顶元素一半的元素)。最后将两个堆合并成一个堆并返回堆顶元素即可。
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x7FFFFFFF;
const int MOD = 1e9 + 7;
const double EPS = 1e-10;
const double PI = 2 * acos (0.0);
const int maxn = 1e5 + 66;
struct node{
int key, lson, rson;
};
node tr[maxn];
int par[maxn];
void Init (){
memset (tr, 0, sizeof (tr));
for (int i = 0; i < maxn; i++)
par[i] = i;
}
int Merge (int a, int b){
if (!a) return b;
if (!b) return a;
if (tr[a].key < tr[b].key) swap (a, b);
tr[a].rson = Merge (tr[a].rson, b);
par[tr[a].rson] = a;
swap (tr[a].rson, tr[a].lson);
return a;
}
int Del (int a){
int lch = tr[a].lson, rch = tr[a].rson;
par[lch] = lch, par[rch] = rch;
tr[a].lson = tr[a].rson = 0;
return Merge (lch, rch);
}
int UnFind (int val){
if (par[val] == val)
return val;
return par[val] = UnFind (par[val]);
}
int main(){
int n;
while (cin >> n){
Init ();
for (int i = 1; i <= n; i++)
cin >> tr[i].key;
int q;
cin >>q;
for (int i = 1; i <= q; i++){
int u, v;
cin >> u >> v;
u = UnFind (u);
v = UnFind (v);
if(u == v)
cout << "-1" << endl;
else{
int ta = Del (u);
int tb = Del (v);
tr[u].key /= 2;
tr[v].key /= 2;
ta = Merge (u, ta);
tb = Merge (v, tb);
int tt = Merge (ta, tb);
cout << tr[tt].key << endl;
}
}
}
return 0;
}
图形结构
一个图(G)定义为一个偶对(V,E),记为G=(V,E):
- V是顶点(Vertex)的非空有限集合,记为V(G)
- E是无序集V&V的一个子集,记为E(G),其元素是图的弧(Arc)
- 将顶点集合为空的图称为空图
- 弧:表示两个顶点v和w之间存在一个关系,用顶点偶对<v,w>表示
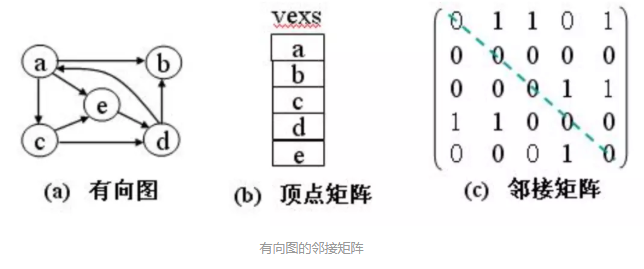
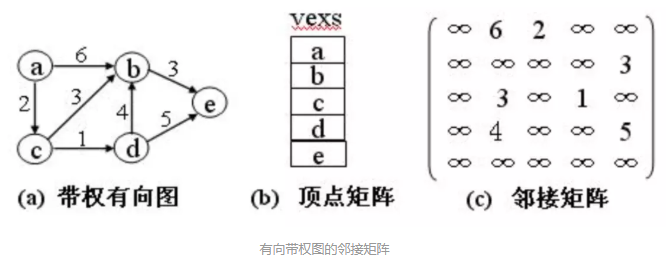
邻接矩阵
基本思想:对于有n个顶点的图,用一维数组vexs[n]存储顶点信息,用二维数组A[n][n]存储顶点之间关系的信息。该二维数组称为邻接矩阵。
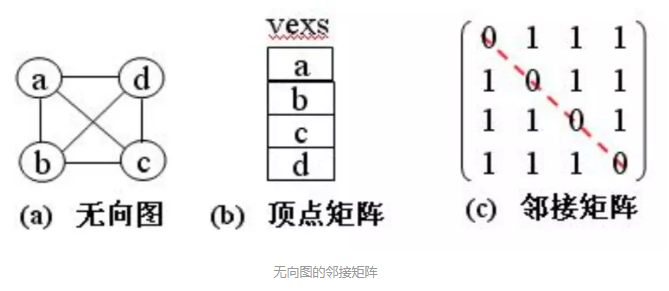
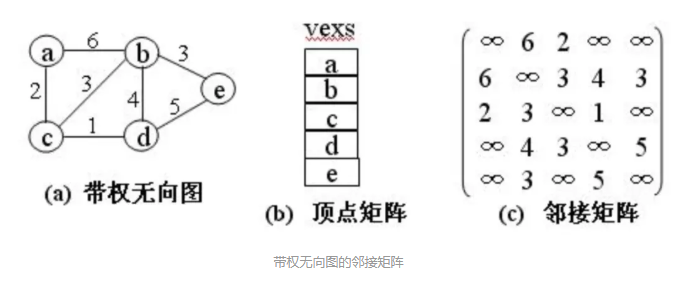
#include <bits/stdc++.h>
using namespace std;
#define INFINITY 65535//定义无穷
#define MAX_VEX 30 //最大顶点数目
typedef enum {
DG, AG, WDG, WAG //{有向图,无向图,带权有向图,带权无向图}
} GraphKind;
typedef struct {
GraphKind kind; /* 图的种类标志 */
int verxtexNum, arcNum; /* 图的当前顶点数和弧数 */
char vexs[MAX_VEX]; //顶点集合
int edges[MAX_VEX][MAX_VEX];//邻接矩阵
} MGraph;/* 图的结构定义 */
//图的创建
MGraph *createGraph(MGraph *G) {
printf("请输入图的种类标志:");
scanf("%d", &G->kind);
G->verxtexNum = 0; /* 初始化顶点个数 */
return (G);
}
//图的顶点定位,实际上是确定一个顶点在 vexs 数组中的位置(下标) ,其过程完全等同于在顺序存储的线性表中查找一个数据元素。
int LocateVex(MGraph *G, char ch) {
for (int i = 0; i < G->verxtexNum; i++) {
if (G->vexs[i] == ch) {
return (i);
}
}
return (-1); /*图中无此顶点*/
}
//向图中增加顶点,类似在顺序存储的线性表的末尾增加一个数据元素。
int addVertex(MGraph *G, char ch) {
int j, k;
if (G->verxtexNum >= MAX_VEX) {
printf("Vertex overflow!\n");
return (-1);
}
if (LocateVex(G, ch) != -1) {
printf("Vertex has existed!\n");
return (-1);
}
k = G->verxtexNum;
G->vexs[G->verxtexNum++] = ch;
if (G->kind == DG || G->kind == AG) {//不带权
for (j = 0; j < G->verxtexNum; j++) {//新加一行和一列
G->edges[j][k] = G->edges[k][j] = 0;
}
} else {
for (j = 0; j < G->verxtexNum; j++) {
G->edges[j][k] = G->edges[k][j] = INFINITY;
}
}
return (k);
}
//向图中增加一条弧,根据给定的弧或边所依附的顶点,修改邻接矩阵中所对应的数组元素。
int addArc(MGraph *G, char ch1, char ch2, int weight) {
int j = LocateVex(G, ch1);
int k = LocateVex(G, ch2);
if (k == -1 || j == -1) {
printf("Vertex do not exist!\n");
return (-1);
}
if (G->kind == DG || G->kind == WDG) {//有向图
G->edges[j][k] == weight;
} else {//无向图
G->edges[j][k] == weight;
G->edges[k][j] == weight;
}
return (1);
}
【POJ 2387】Til the Cows Come Home
对于邻接矩阵,这题有重边,加一个判重,存重边中短的。
#include <bits/stdc++.h>
using namespace std;
int M[1050][1050],T,N,dist[1050];
bool visit[1050];
void dijkstra(){
memset(visit,false,sizeof(visit));
for(int i=1;i<=N;i++)
dist[i]=M[1][i];
visit[1]=true;
for(int i=2;i<=N;i++){
int Min=inf,index;
for(int j=1;j<=N;j++){
if(visit[j]==false&&dist[j]<Min){
index=j;
Min=dist[j];
}
}
visit[index]=true;
for(int j=1;j<=N;j++){
if(visit[j]==false&&dist[j]>dist[index]+M[index][j])
dist[j]=dist[index]+M[index][j];
}
}
}
int main(){
while(~scanf("%d %d",&T,&N)){
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++)
if(i==j) M[i][j]=0;
else M[i][j]=inf;
for(int i=1;i<=T;i++){
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
if(M[a][b]>c)
M[a][b]=M[b][a]=c;
}
dijkstra();
printf("%d\n",dist[N]);
}
}
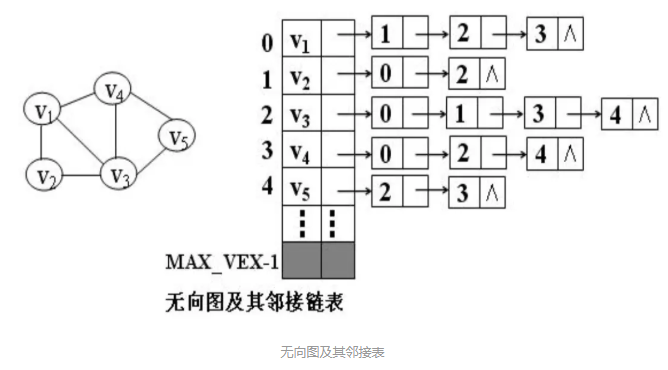
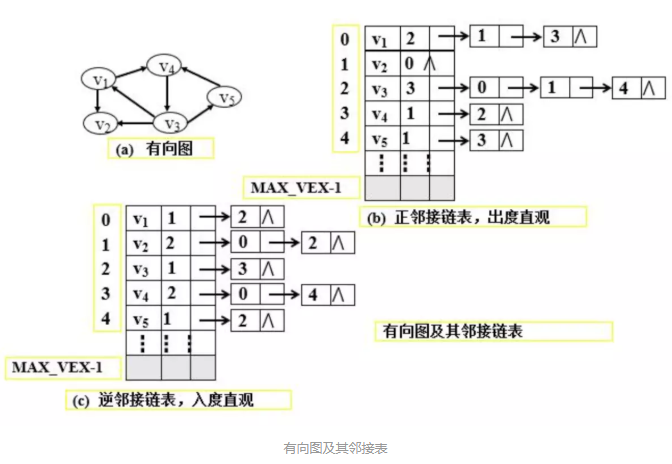
邻接表
基本思想:类似于树的孩子链表法,就是对于图 G 中的每个顶点vi,将所有邻接于vi的顶点vj链成一个单链表,这个单链表就称为顶点vi的邻接链表,再将所有点的邻接表表头放到数组中,就构成了图的邻接链表。

- 顶点表的结点:由顶点域(data)和指向第一条邻接边的指针域(firstarc) 构成。
- 边表结点(即邻接表):由邻接点域(adjvex)和指向下一条邻接边的指针域(nextarc)构成。
#include <bits/stdc++.h>
using namespace std;
#define MAX_VEX 30 /* 最大顶点数 */
typedef enum {
DG, AG, WDG, WAG
} GraphKind;
typedef struct LinkNode {
int adjvex;//邻接点在头结点数组中的位置(下标)
int weight;//权值
struct LinkNode *nextarc;//指向下一个表结点
} LinkNode;/*表结点类型定义 */
typedef struct VexNode {
char data; // 顶点信息
LinkNode *firstarc; // 指向第一个表结点
} VexNode;/* 顶点结点类型定义 */
typedef struct {
GraphKind kind;/*图的种类标志 */
int vexnum;//顶点数
VexNode AdjList[MAX_VEX];//邻接表
} ALGraph;/* 图的结构定义 */
//图的创建
ALGraph *createGraph(ALGraph *G) {
printf("请输入图的种类标志:");
scanf("%d", &G->kind);
G->vexnum = 0; /*初始化顶点个数*/
return (G);
}
//顶点定位,确定一个顶点在 AdjList 数组中的某个元素的 data 域内容。
int LocateVex(ALGraph *G, char ch) {
for (int i = 0; i < G->vexnum; i++) {
if (G->AdjList[i].data == ch) {
return (i);
}
}
return (-1);/* 图中无此顶点*/
}
//向图中增加顶点,在 AdjList 数组的末尾增加一个数据元素。
int AddVertex(ALGraph *G, char ch) {
int k;
if (G->vexnum >= MAX_VEX) {
printf("Vertex Overflow !\n");
return (-1);
}
if (LocateVex(G, ch) != -1) {
printf("Vertex has existed !\n");
return (-1);
}
G->AdjList[G->vexnum].data = ch;
G->AdjList[G->vexnum].firstarc = NULL;
k = ++G->vexnum;
return k;
}
//向图中增加一条弧,根据给定弧或边所依附的顶点,修改单链表,无向图修改两个单链表;有向图修改一个单链表。
int addArc(ALGraph *G, char ch1, char ch2, int weight) {
int k, j;
LinkNode *p, *q;
k = LocateVex(G, ch1);
j = LocateVex(G, ch2);
if (k == -1 || j == -1) {
printf("Arc’s Vertex do not exist!\n");
return (-1);
}
p = (LinkNode *) malloc(sizeof(LinkNode));
p->weight = weight;
q = (LinkNode *) malloc(sizeof(LinkNode));
q->weight = weight;
if (G->kind == AG || G->kind == WAG) {//无向图,用头插入法插入到两个单链表
p->nextarc = G->AdjList[k].firstarc;
G->AdjList[k].firstarc = p;
q->nextarc = G->AdjList[j].firstarc;
G->AdjList[j].firstarc = q;
} else {
p->nextarc = G->AdjList[k].firstarc;
G->AdjList[k].firstarc = p; /*建立正邻接链表用 */
//q->nextarc = G->AdjList[j].firstarc;
//G->AdjList[j].firstarc = q;/*建立逆邻接链表用 */
}
return (1);
}
【POJ 2387】Til the Cows Come Home
对于邻接表,写法稍与邻接矩阵不同,这里dist初始化并不是存起始点到各个边的距离,而是都初始化无穷大。 然后这里最初是先用起始点松弛(其实是找离起始点最短的边,有重边也没关系),再找最短边加入,再用这个最短边到达的点去松弛其他边。 所以这里松弛的作用,起到去重边也能把最短边入dist数组。
#include <bits/stdc++.h>
using namespace std;
#define inf 1<<29
const int maxn=4050;
int u[maxn],v[maxn],w[maxn],first[maxn],next[maxn],T,N,dist[maxn];
bool visit[maxn];
void dijkstra(){
memset(visit,false,sizeof(visit));
for(int i=1;i<=N;i++)
dist[i]=inf;
dist[1]=0;
visit[1]=true;
int Min,index=1;
for(int i=2;i<=N;i++){
for(int j=first[index];j!=-1;j=next[j]){
if(visit[v[j]]==false&&dist[index]+w[j]<dist[v[j]])
dist[v[j]]=dist[index]+w[j];
}
Min=inf;
for(int j=1;j<=N;j++){
if(visit[j]==false&&dist[j]<Min){
index=j;
Min=dist[j];
}
}
visit[index]=true;
}
}
int main(){
while(~scanf("%d %d",&T,&N)){
memset(first,-1,sizeof(first));
memset(next,-1,sizeof(next));
for(int i=1;i<=T*2;i+=2){
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
u[i]=v[i+1]=a,v[i]=u[i+1]=b,w[i]=w[i+1]=c;//无向边,双向存。
next[i]=first[u[i]],next[i+1]=first[u[i+1]];
first[u[i]]=i,first[u[i+1]]=i+1;
}
dijkstra();
printf("%d\n",dist[N]);
}
}
十字链表
十字链表(Orthogonal List)是有向图的另一种链式存储结构,是将有向图的正邻接表和逆邻接表结合起来得到的一种链表。
在这种结构中,每条弧的弧头结点和弧尾结点都存放在链表中,并将弧结点分别组织到以弧尾结点为头(顶点)结点和以弧头结点为头(顶点)结点的链表中。

- data 域:存储和顶点相关的信息
- 指针域 firstin:指向以该顶点为弧头的第一条弧所对应的弧结点,即逆邻接链表
- 指针域 firstout:指向以该顶点为弧尾的第一条弧所对应的弧结点,即正邻接链表
- 尾域 tailvex:指示弧尾顶点在图中的位置
- 头域 headvex:指示弧头顶点在图中的位置
- 指针域 hlink:指向弧头相同的下一条弧
- 指针域 tlink:指向弧尾相同的下一条弧
- Info 域:指向该弧的相关信息,比如权值
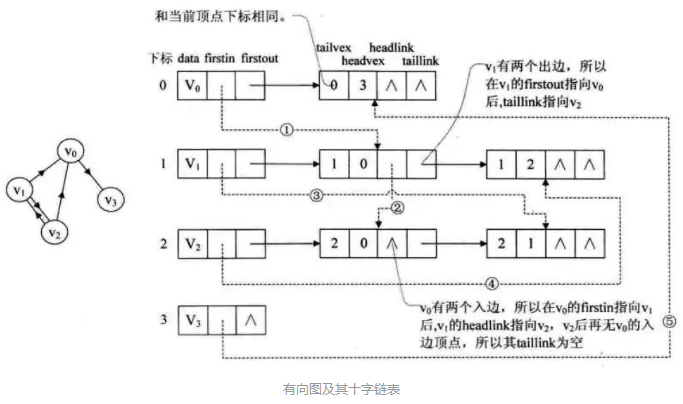
实质就是先把图的正邻接链表(出度)画出来,然后再把firstin,firstout,hlink,tlink连起来。
#include <bits/stdc++.h>
using namespace std;
#define MAX_VEX 30 /* 最大顶点数 */
#define INFINITY 65535/* 最大值∞ */
#define MAX_VEX 30//最大顶点数
typedef struct ArcNode {
int tailvex, headvex;//尾结点和头结点在图中的位置
int info;//权值
struct ArcNode *hlink, *tlink;
} ArcNode;/* 弧结点类型定义 */
typedef struct VexNode {
char data; // 顶点信息
ArcNode *firstin, *firstout;
} VexNode;/* 顶点结点类型定义 */
typedef struct {
int vexnum;
VexNode xlist[MAX_VEX];
} OLGraph; /* 图的类型定义 */
十字交叉双向循环链表dancing links
#include <bits/stdc++.h>
using namespace std;
int m, n, num[17][301];
const int maxx = 6000, mr = 17;
int key, up[maxx], down[maxx], lef[maxx], rig[maxx];//上下左右
int row[maxx], col[maxx], rhead[mr];//行,列,每行第一个元素
void init(){
for (int i = 0; i <= n; i++){
up[i] = i, down[i] = i;
lef[i] = i - 1, rig[i] = i + 1;
row[i] = 0, col[i] = i;
}
lef[0] = n, rig[n] = 0;
key = n;
for (int i = 0; i <= m; i++)rhead[i] = 0;
}
void push(int r, int c){//新增坐标在(r,c)的一个节点
row[++key] = r, col[key] = c;
up[key] = c, down[key] = down[c];
up[down[c]] = key, down[c] = key;
if (rhead[r] == 0)rhead[r] = lef[key] = rig[key] = key;
else{
lef[key] = rhead[r], rig[key] = rig[rhead[r]];
lef[rig[rhead[r]]] = key, rig[rhead[r]] = key;
}
}
void del(int c){//删除第c列的所有元素和他们所在行的所有元素
lef[rig[c]] = lef[c], rig[lef[c]] = rig[c];
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = down[j], up[down[j]] = up[j];
}
void reback(int c){
lef[rig[c]] = rig[lef[c]] = c;
for (int i = down[c]; i != c; i = down[i])
for (int j = rig[i]; j != i; j = rig[j])
down[up[j]] = up[down[j]] = j;
}
bool dfs(){
if (rig[0] == 0)return true;
int c = rig[0];
del(c);
for (int i = down[c]; i != c; i = down[i]){
for (int j = rig[i]; j != i; j = rig[j])del(col[j]);
if (dfs())return true;
for (int j = rig[i]; j != i; j = rig[j])reback(col[j]);
}
reback(c);
return false;
}
int main(){
while (scanf("%d%d",&m,&n)!=EOF){
init();
for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++){
scanf("%d", &num[i][j]);
if (num[i][j])push(i, j);
}
if (dfs())printf("Yes, I found it\n");
else printf("It is impossible\n");
}
return 0;
}
邻接多重表
邻接多重表(Adjacency Multilist)是无向图的另一种链式存储结构。 邻接多重表的结构和十字链表类似,每条边用一个结点表示。 邻接多重表中的顶点结点结构与邻接表中的完全相同,而表结点包括六个域。

- data 域:存储和顶点相关的信息
- 指针域 firstedge:指向依附于该顶点的第一条边所对应的表结点
- 标志域 mark:用以标识该条边是否被访问过
- ivex 和 jvex 域:分别保存该边所依附的两个顶点在图中的位置
- info 域:保存该边的相关信息
- 指针域 ilink:指向下一条依附于顶点 ivex 的边
- 指针域 jlink:指向下一条依附于顶点 jvex 的边
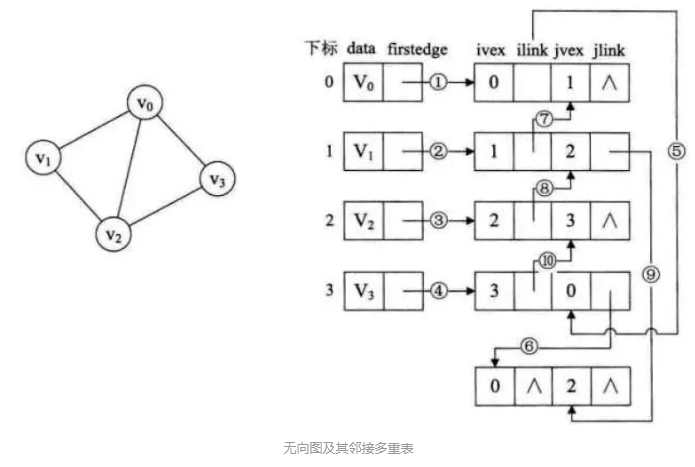
邻接表的同一条边用两个表结点表示,而邻接多重表只用一个表结点表示;除标志域外,邻接多重表与邻接表表达的信息是相同的。
#include <bits/stdc++.h>
using namespace std;
#define MAX_VEX 30 /* 最大顶点数 */
typedef enum {
unvisited, visited
} Visitting;
typedef struct EdgeNode {
Visitting mark; // 访问标记
int ivex, jvex; // 该边依附的两个结点在图中的位置
int weight; //权值
struct EdgeNode *ilink, *jlink;// 分别指向依附于这两个顶点的下一条边
} EdgeNode; /* 弧边结点类型定义 */
typedef struct VexNode {
char data; // 顶点信息
EdgeNode *firsedge; // 指向依附于该顶点的第一条边
} VexNode;/* 顶点结点类型定义 */
typedef struct {
int vexnum;
VexNode mullist[MAX_VEX];
} AMGraph;