Last updated on 2019-03-30…
搜索其实涵盖很多内容,比如排序、数据积累、页面解析、超链分析、上亿量级的站点分级、黄赌毒暴识别、多维度评测等等,每个点都可以做的很细,本文仅以绝对简略的方式探讨一下。
核心结构
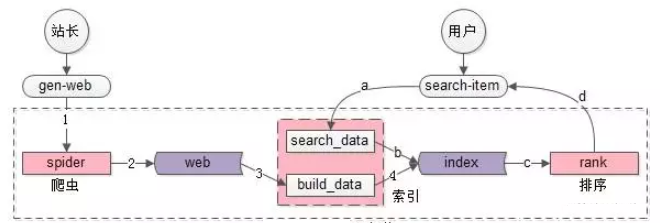
- 核心数据主要分为两部分(紫色部分):web网页库、index索引数据。
- spider和search&index是相对工程的系统
- rank是和业务、策略紧密、算法相关的系统,搜索体验的差异主要在此,而业务、策略的优化是需要时间积累的
spider爬虫
- spider把互联网网页抓过来
- spider把互联网网页存储到网页库中(这个对存储的要求很高,要存储几乎整个“万维网”的镜像)
search&index索引与查询
建立索引与查询索引系统,这个系统又主要分为两部分:
一部分用于生成索引数据build_index
- build_index从网页库中读取数据,完成分词
- build_index生成倒排索引
一部分用于查询索引数据search_index
- search_index获得用户的搜索词,完成分词
- search_index查询倒排索引,获得“字符匹配”网页,这是初筛的结果
将搜索词分词后,索引结构通常建立为<词, 文档编号, tf>形式,若以mapreduce处理,则key为词,value为tf+文档编号。
rank打分排序
输入:用户的搜索词。输出:排好序的第一页检索结果。
- rank对初筛的结果进行打分排序
- rank对排序后的第一页结果返回
检索的过程
分词、查倒排索引、求结果集交集
假设搜索词是“我爱”:
1、分词,“我爱”会分词为{我,爱},时间复杂度为O(1)
2、每个分词后的item,从倒排索引查询包含这个item的网页list
- 我 -> {url1, url2, url3}
- 爱 -> {url2, url3, url4}
3、求list
分词和倒排查询时间复杂度都是O(1),整个搜索的时间复杂度取决于“求list
的交集”,问题转化为了求**两个集合交集**。
有序集合求交集
两层for O(n2)
每个搜索词命中的网页是很多的,O(n*n)的复杂度是明显不能接受的。倒排索引是在创建之初可以进行排序预处理,问题转化成两个有序的list求交集,就方便多了。
拉链法 O(n2)
前提:有序list求交集
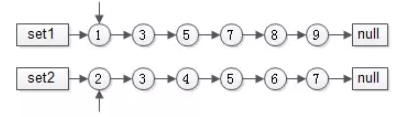
两个指针指向首元素,比较元素的大小:
- 如果相同,放入结果集,随意移动一个指针
- 否则,移动值较小的一个指针,直到队尾
这种方法的好处是:
- 集合中的元素最多被比较一次,时间复杂度为O(n)
- 多个有序集合可以同时进行,这适用于多个分词的item求url_id交集
这个方法就像一条拉链的两边齿轮,一一比对就像拉链,故称为拉链法。 倒排索引是提前初始化的,可以利用“有序”这个特性。
分桶并行优化
数据量大时,url_id分桶水平切分+并行运算是一种常见的优化方法。
如果能将list1
举例:
有序集合1{1,3,5,7,8,9, 10,30,50,70,80,90}
有序集合2{2,3,4,5,6,7, 20,30,40,50,60,70}
求交集,先进行分桶拆分:
桶1的范围为[1, 9]
桶2的范围为[10, 100]
桶3的范围为[101, max_int]
于是:
集合1就拆分成
集合a{1,3,5,7,8,9}
集合b{10,30,50,70,80,90}
集合c{}
集合2就拆分成
集合d{2,3,4,5,6,7}
集合e{20,30,40,50,60,70}
集合e{}
每个桶内的数据量大大降低了,并且每个桶内没有重复元素,可以利用多线程并行计算:
桶1内的集合a和集合d的交集是x{3,5,7}
桶2内的集合b和集合e的交集是y{30, 50, 70}
桶3内的集合c和集合d的交集是z{}
最终,集合1和集合2的交集,是x与y与z的并集,即集合{3,5,7,30,50,70}。
多线程、水平切分都是常见的优化手段。
bitmap再次优化 O(n)
数据进行了水平分桶拆分之后,每个桶内的数据一定处于一个范围之内,如果集合符合这个特点,就可以使用bitmap来表示集合:
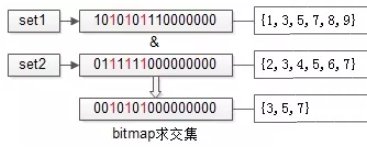
如上图,假设set1{1,3,5,7,8,9}和set2{2,3,4,5,6,7}的所有元素都在桶值[1, 16]的范围之内,可以用16个bit来描述这两个集合。
原集合中的元素x,在这个16bitmap中的第x个bit为1,此时两个bitmap求交集,只需要将两个bitmap进行“与”操作,结果集bitmap的3,5,7位是1,表明原集合的交集为{3,5,7}。
水平分桶,bitmap优化之后,能极大提高求交集的效率,但时间复杂度仍旧是O(n)。bitmap需要大量连续空间,占用内存较大。
bitmap能够表示集合,用它求集合交集速度非常快。
skiplist跳表 O(log(n))
有序链表集合求交集,跳表是最常用的数据结构,它可以将有序集合求交集的复杂度由O(n)降至接近O(log(n))。
要求交集,如果用拉链法,会发现1,2,3,4,20,21,22,23都要被无效遍历一次,每个元素都要被比对,时间复杂度为O(n),能不能每次比对“跳过一些元素”呢?
跳表就出现了:
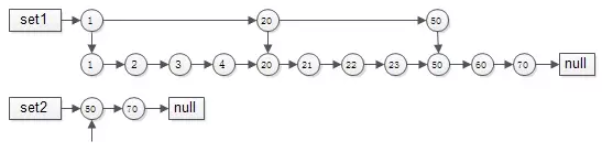
- 集合1{1,2,3,4,20,21,22,23,50,60,70}建立跳表时,一级只有{1,20,50}三个元素,二级与普通链表相同。
- 集合2{50,70}由于元素较少,只建立了一级普通链表。
如此这般,在实施“拉链”求交集的过程中,set1的指针能够由1跳到20再跳到50,中间能够跳过很多元素,无需进行一一比对,跳表求交集的时间复杂度近似O(log(n)),这是搜索引擎中常见的算法。
搜索架构发展
原始阶段-LIKE
创业阶段,常常用这种方法来快速实现。
数据在数据库中可能是这么存储的:t_tiezi(tid, title, content)
满足标题、内容的检索需求可以通过LIKE实现:select tid from t_tiezi where content like ‘%baidu%’
这种方式确实能够快速满足业务需求,存在的问题也显而易见:
- 效率低,每次需要全表扫描,计算量大,并发高时cpu容易100%
- 不支持分词
初级阶段-全文索引
如何快速提高效率,支持分词,并对原有系统架构影响尽可能小呢,第一时间想到的是建立全文索引:alter table t_tiezi add fulltext(title,content)
使用match和against实现索引字段上的查询需求。
全文索引能够快速实现业务上分词的需求,并且快速提升性能(分词后倒排,至少不要全表扫描了),但也存在一些问题:
- 只适用于MyISAM
- 由于全文索引利用的是数据库特性,搜索需求和普通CURD需求耦合在数据库中:检索需求并发大时,可能影响CURD的请求;CURD并发大时,检索会非常的慢
- 数据量达到百万级别,性能还是会显著降低,查询返回时间很长,业务难以接受
- 比较难水平扩展
中级阶段-开源外置索引
为了解决全文索的局限性,当数据量增加到大几百万,千万级别时,就要考虑外置索引了。外置索引的核心思路是:索引数据与原始数据分离,前者满足搜索需求,后者满足CURD需求,通过一定的机制(双写,通知,定期重建)来保证数据的一致性。
原始数据可以继续使用Mysql来存储,外置索引如何实施?Solr,Lucene,ES都是常见的开源方案。其中,ES(ElasticSearch)是目前最为流行的。
Lucene虽好,潜在的不足是:
- Lucene只是一个库,需要自己做服务,自己实现高可用/可扩展/负载均衡等复杂特性
- Lucene只支持Java,如果要支持其他语言,必须得自己做服务
- Lucene不友好,这是很致命的,非常复杂,使用者往往需要深入了解搜索的知识来理解它的工作原理,为了屏蔽其复杂性,还是得自己做服务
为了改善Lucene的各项不足,解决方案都是“封装一个接口友好的服务,屏蔽底层复杂性”,于是有了ES
- ES是一个以Lucene为内核来实现搜索功能,提供REStful接口的服务
- ES能够支持很大数据量的信息存储,支持很高并发的搜索请求
- ES支持集群,向使用者屏蔽高可用/可扩展/负载均衡等复杂特性
高级阶段-自研搜索引擎
当数据量进一步增加,达到10亿、100亿数据量;并发量也进一步增加,达到每秒10万吞吐量;业务个性也逐步增加的时候,就需要自研搜索引擎了,定制化实现搜索内核了。
到了定制化自研搜索引擎的阶段,超大数据量、超高并发量为设计重点,为了达到“无限容量、无限并发”的需求,架构设计需要重点考虑“扩展性”,力争做到:增加机器就能扩容(数据量+并发量)。
- 为了满足数据容量的扩展性,索引数据进行了水平切分,增加切分份数,就能够无限扩展性能,如上图searcher分为了4组
- 为了满足一份数据的性能扩展性,同一份数据进行了冗余,理论上做到增加机器就无限扩展性能
实时搜索引擎
大数据量、高并发量情况下的搜索引擎为了保证实时性,架构设计上的两个要点:
- 索引分级
- dump&merge
首先,在数据量非常大的情况下,为了保证倒排索引的高效检索效率,任何对数据的更新,并不会实时修改索引。因为,一旦产生碎片,会大大降低检索效率。
既然索引数据不能实时修改,如何保证最新的网页能够被索引到呢?
- 索引分级
- 分为全量库
- 日增量库
- 小时增量库。